题目内容
【题目】设函数f(x)=4x3+ ![]() ,x∈[0,1],证明:
,x∈[0,1],证明:
(Ⅰ)f(x)≥1﹣2x+3x2;
(Ⅱ) ![]() <f(x)≤
<f(x)≤ ![]() .
.
【答案】证明:(I)令g(x)=(1+x)2(1﹣2x+3x2﹣4x3),x∈[0,1],
则g′(x)=﹣20(1+x)x3≤0,当且仅当x=0时取等号,
∴g(x)在[0,1]上单调递减,故g(x)≤g(0)=1,
∴(1+x)2(1﹣2x+3x2﹣4x3)≤1,
∴ ![]() ≥1﹣2x+3x2,
≥1﹣2x+3x2,
即f(x)≥1﹣2x+3x2.
(II)由(I)知f(x)≥1﹣2x+3x2=3(x﹣ ![]() )2≥
)2≥ ![]() ,
,
∵两处等号不能同时成立,
∴f(x)> ![]() .
.
f′(x)=12x2﹣ ![]() =
= 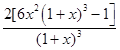 ,
,
令h(x)=6x2(1+x)3﹣1,则f(x)在[0,1]上单调递增,
∵h(0)=﹣1,h(1)=47>0,
∴h(x)在(0,1)上存在唯一一个零点x0,
∴当0<x<x0时,f′(x)<0,当x0<x<1时,f′(x)>0,
∴f(x)在[0,1]上先减后增,
又f(0)=1,f(1)= ![]() ,
,
∴f(x)≤f(1)= ![]() .
.
综上, ![]() f(x)≤
f(x)≤ ![]()
【解析】(I)构造函数g(x)=(1+x)2(1﹣2x+3x2﹣4x3),判断g(x)的单调性得出最大值,化简即可得出结论;(II)判断f(x)的单调性即可f(x)的最大值,利用(I)得出f(x)> ![]() .
.
【考点精析】本题主要考查了不等式的证明的相关知识点,需要掌握不等式证明的几种常用方法:常用方法有:比较法(作差,作商法)、综合法、分析法;其它方法有:换元法、反证法、放缩法、构造法,函数单调性法,数学归纳法等才能正确解答此题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


