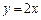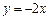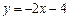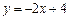题目内容
(本题满分14分)已知函数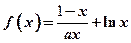
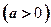 。
。
(Ⅰ)若函数 在
在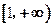 上为增函数,求正实数
上为增函数,求正实数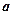 的取值范围;
的取值范围;
(Ⅱ)当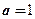 时,求
时,求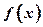 在
在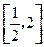 上的最大值和最小值;
上的最大值和最小值;
(Ⅲ)当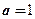 时,求证:对大于
时,求证:对大于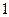 的任意正整数
的任意正整数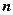 ,都有
,都有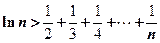 。
。
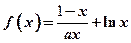
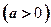 。
。(Ⅰ)若函数
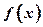 在
在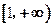 上为增函数,求正实数
上为增函数,求正实数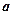 的取值范围;
的取值范围;(Ⅱ)当
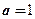 时,求
时,求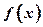 在
在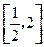 上的最大值和最小值;
上的最大值和最小值;(Ⅲ)当
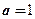 时,求证:对大于
时,求证:对大于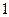 的任意正整数
的任意正整数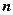 ,都有
,都有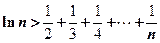 。
。解:(I)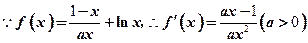 ……………1分
……………1分
∵ 函数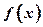 在
在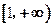 上为增函数
上为增函数
∴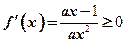 对
对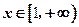 恒成立, ……………………2分
恒成立, ……………………2分
∴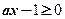 对
对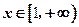 恒成立,即
恒成立,即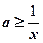 对
对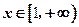 恒成立
恒成立
∴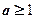 ……………………4分
……………………4分
(II)当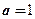 时,
时,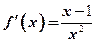 ,
,
∴ 当 时,
时,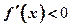 ,故
,故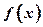 在
在 上单调递减;当
上单调递减;当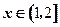 时,
时,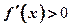 ,故
,故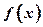 在
在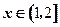 上单调递增, ………………6分
上单调递增, ………………6分
∴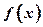 在区间
在区间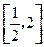 上有唯一极小值点,故
上有唯一极小值点,故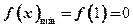 ……7分
……7分
又
∵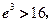 ∴
∴ 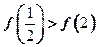
∴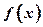 在区间
在区间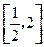 上的最大值
上的最大值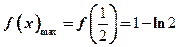
综上可知,函数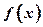 在
在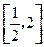 上的最大值是
上的最大值是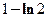 ,最小值是
,最小值是
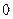 。………………9分
。………………9分
(Ⅲ)当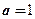 时,
时,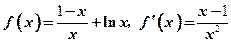 ,故
,故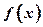 在
在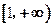 上为增函数。
上为增函数。
当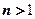 时,令
时,令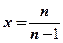 ,则
,则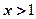 ,故
,故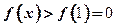 ……………………11分
……………………11分
∴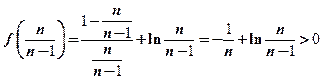 即
即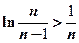 ………12分
………12分
∴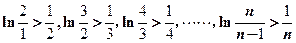
∴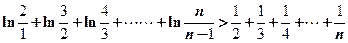 …………………13分
…………………13分
∴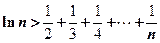
即对大于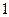 的任意正整数
的任意正整数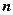 ,都有
,都有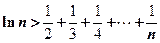 ……………………14分
……………………14分
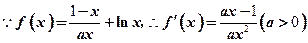 ……………1分
……………1分∵ 函数
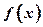 在
在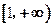 上为增函数
上为增函数∴
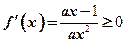 对
对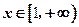 恒成立, ……………………2分
恒成立, ……………………2分∴
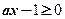 对
对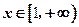 恒成立,即
恒成立,即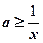 对
对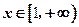 恒成立
恒成立∴
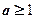 ……………………4分
……………………4分(II)当
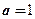 时,
时,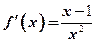 ,
,∴ 当
 时,
时,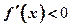 ,故
,故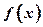 在
在 上单调递减;当
上单调递减;当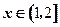 时,
时,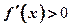 ,故
,故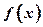 在
在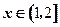 上单调递增, ………………6分
上单调递增, ………………6分∴
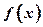 在区间
在区间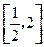 上有唯一极小值点,故
上有唯一极小值点,故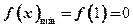 ……7分
……7分又

∵
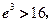 ∴
∴ 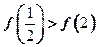
∴
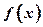 在区间
在区间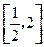 上的最大值
上的最大值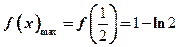
综上可知,函数
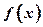 在
在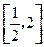 上的最大值是
上的最大值是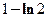 ,最小值是
,最小值是
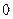 。………………9分
。………………9分(Ⅲ)当
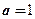 时,
时,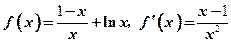 ,故
,故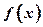 在
在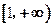 上为增函数。
上为增函数。当
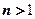 时,令
时,令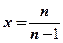 ,则
,则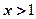 ,故
,故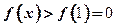 ……………………11分
……………………11分∴
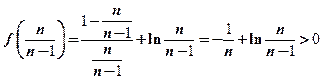 即
即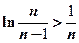 ………12分
………12分∴
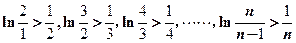
∴
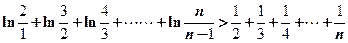 …………………13分
…………………13分∴
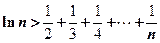
即对大于
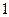 的任意正整数
的任意正整数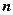 ,都有
,都有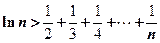 ……………………14分
……………………14分略

练习册系列答案
相关题目
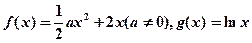 .
.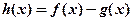 存在单调增区间,求
存在单调增区间,求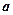 的取值范围;
的取值范围;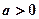 ,使得方程
,使得方程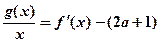 在区间
在区间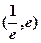 内有且只有两个不相等的实数根?若存在,求出
内有且只有两个不相等的实数根?若存在,求出 要在公园内建一块顶点都在圆P上的多边形活动场地.
要在公园内建一块顶点都在圆P上的多边形活动场地.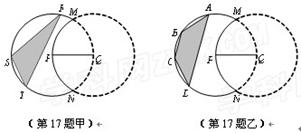
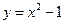 ,直线
,直线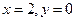 所围成的图形的面积
所围成的图形的面积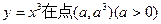 处的切线与x轴、直线
处的切线与x轴、直线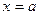 所围成的三角形的面积为
所围成的三角形的面积为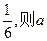 = .
= .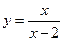 ,在点
,在点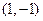
 处的切线方程为
处的切线方程为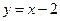
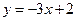
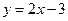
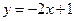
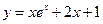 在点(0,1)处的切线方程为
在点(0,1)处的切线方程为  B (log2x)′=
B (log2x)′=
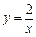 的图象在点
的图象在点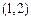 处的切线方程是( )
处的切线方程是( )