题目内容
圆 内有一点P(-1,2),AB过点P,若弦长
内有一点P(-1,2),AB过点P,若弦长
①求直线AB的倾斜角 ;
;
②若圆上恰有三点到直线AB的距离等于 ,求直线AB的方程.
,求直线AB的方程.
 内有一点P(-1,2),AB过点P,若弦长
内有一点P(-1,2),AB过点P,若弦长
①求直线AB的倾斜角
 ;
;②若圆上恰有三点到直线AB的距离等于
 ,求直线AB的方程.
,求直线AB的方程.(1)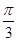 或
或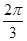 ; (2)x+y-1=0或x-y+3=0.
; (2)x+y-1=0或x-y+3=0.
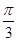 或
或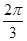 ; (2)x+y-1=0或x-y+3=0.
; (2)x+y-1=0或x-y+3=0.试题分析:①设圆心(-1,0)到直线AB的距离为d,则 d=
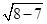 =1,设直线AB的倾斜角α,斜率为k,则直线AB的方程 y-2=k(x+1),即 kx-y+k+2=0,d=1=
=1,设直线AB的倾斜角α,斜率为k,则直线AB的方程 y-2=k(x+1),即 kx-y+k+2=0,d=1=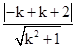 ,
,∴k=
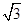 或-
或-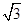 ,∴直线AB的倾斜角α=60°或 120°.
,∴直线AB的倾斜角α=60°或 120°.②∵圆上恰有三点到直线AB的距离等于
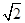 ,
,∴圆心(-1,0)到直线AB的距离d=
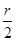 =
=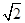 ,
,直线AB的方程 y-2=k(x+1),
即kx-y+k+2=0,
由d=
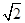 =
=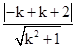 ,
,解可得k=1或-1,
直线AB的方程 x-y+3=0 或-x-y+1=0.
点评:中档题,确定直线的方程,常用方法是“待定系数法”。本题利用利用点到直线的距离公式,建立斜率的方程求解。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 与⊙
与⊙ 相切,
相切, 为切点,
为切点, 为割线,弦
为割线,弦 ,
, 相交于
相交于 点,
点, 为
为 上一点,且
上一点,且 .
.
 ;
; .
. 与圆C:
与圆C: ,
, 相切,求m的值。
相切,求m的值。 ,求圆C 截直线L所得的弦长。
,求圆C 截直线L所得的弦长。 上一动点,则A到直线
上一动点,则A到直线 的最大距离为______.
的最大距离为______.



 的
的 中,弦
中,弦


 与直线
与直线 及
及 都相切,且圆心在直线
都相切,且圆心在直线 上,则圆
上,则圆 是⊙
是⊙ 的直径,
的直径, 是
是 ,
, ,若
,若 ,则⊙
,则⊙ __________ .
__________ .
 是圆
是圆 的直径,过
的直径,过 、
、 的两条弦
的两条弦 和
和 相交于点
相交于点 ,若圆
,若圆 ,那么
,那么 的值等于________________.
的值等于________________.