题目内容
已知直线L: 与圆C:
与圆C: ,
,
(1) 若直线L与圆 相切,求m的值。
相切,求m的值。
(2) 若 ,求圆C 截直线L所得的弦长。
,求圆C 截直线L所得的弦长。
 与圆C:
与圆C: ,
,(1) 若直线L与圆
 相切,求m的值。
相切,求m的值。(2) 若
 ,求圆C 截直线L所得的弦长。
,求圆C 截直线L所得的弦长。(1)  (2)
(2)
 (2)
(2)
试题分析:本题第(1)问,由于直线与圆相切,则圆心到直线的距离等于圆的半径,即有
 ,只要解出m即可;第(2)问,先求出圆心到直线的距离
,只要解出m即可;第(2)问,先求出圆心到直线的距离 ,由于原的半径为1,则由勾股定理可求出弦长。
,由于原的半径为1,则由勾股定理可求出弦长。解:(1)
 直线
直线 与圆
与圆 相切,
相切, 圆心
圆心 到直线
到直线 的距离
的距离 ,解得
,解得 
 当
当 时,直线
时,直线 的方程为
的方程为 ,圆心
,圆心 到直线
到直线 的距离
的距离 ,
, 弦长
弦长
点评:此题考查了直线与圆的位置关系,涉及的知识有:圆的标准方程,以及点到直线的距离公式,当直线与圆相切时,圆心到直线的距离等于圆的半径,熟练运用此性质是解本题的关键.

练习册系列答案
 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
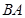 是圆
是圆 的直径,
的直径, 、
、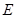 在圆
在圆 、
、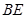 的延长线交直线
的延长线交直线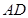 于点
于点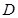 、
、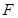 ,
,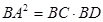 求证:
求证:
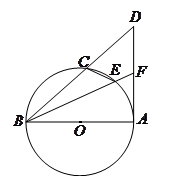
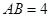 为直径的圆与
为直径的圆与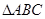 的两边分别交于
的两边分别交于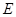 、
、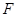 两点,
两点,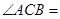
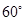 ,则
,则 .
.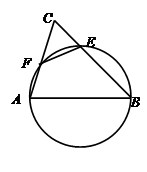
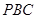 经过圆心
经过圆心 ,
,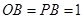 ,
,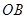 绕点
绕点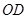 ,连
,连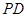 交圆
交圆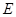 ,则
,则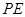 =________.
=________.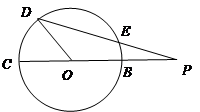
 的半径为3,从圆
的半径为3,从圆 引切线
引切线 和割线
和割线 ,圆心
,圆心 的距离为
的距离为 ,
, ,则切线
,则切线
 内有一点P(-1,2),AB过点P,若弦长
内有一点P(-1,2),AB过点P,若弦长
 ;
; ,求直线AB的方程.
,求直线AB的方程.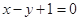 与圆
与圆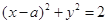 有公共点,则实数a取值范围是( )
有公共点,则实数a取值范围是( ) [1.+∞)
[1.+∞)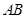 是
是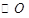 的直径,
的直径,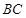 是
是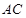 与
与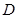 ,若
,若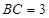 ,
,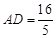 ,则
,则