题目内容
17.在某项测量中,测量结果X服从正态分布N(2,σ2),若X在(0,4)内取值的概率为0.6,则X在(0,2)内取值的概率为( )| A. | 0.2 | B. | 0.3 | C. | 0.4 | D. | 0.6 |
分析 根据ξ服从正态分布N(2,σ2),得到曲线的对称轴是直线x=2,根据所给的ξ在(0,4)内取值的概率为0.6,根据正态曲线的对称性知在(0,2)内取值的概率.
解答 解:∵ξ服从正态分布N(2,σ2)
∴曲线的对称轴是直线x=2,
∵ξ在(0,4)内取值的概率为0.6,
∴根据正态曲线的性质知在(0,2)内取值的概率为0.6×$\frac{1}{2}$=0.3.
故选:B.
点评 本题考查正态分布曲线的特点及曲线所表示的意义,主要考查正态曲线的对称性,是一个基础题.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
7.已知an+1-an-3=0,则数列{an}是( )
| A. | 等差数列 | B. | 等比数列 | ||
| C. | 摆动数列 | D. | 既等差数列又等比数列 |
8.程序框图的基本要素为输入、输出、条件和( )
| A. | 判断 | B. | 有向线 | C. | 循环 | D. | 开始 |
12.函数y=-lnx(1≤x≤e2) 的值域是( )
| A. | [0,2] | B. | [-2,0] | C. | [-$\frac{1}{2}$,0] | D. | [0,$\frac{1}{2}$] |
2.函数y=f(x)的图象在点x=5处的切线方程是y=-x+8,则f(5)+f′(5)=( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
6.已知条件p:|5x-2|>3,q:$\frac{1}{{x}^{2}+4x-5}>0$,则“¬p”是“¬q”成立的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
7.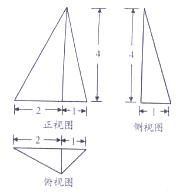 若某几何体的三视图如图所示,则该几何体的体积为( )
若某几何体的三视图如图所示,则该几何体的体积为( )
 若某几何体的三视图如图所示,则该几何体的体积为( )
若某几何体的三视图如图所示,则该几何体的体积为( )| A. | 1 | B. | $\frac{4}{3}$ | C. | 2 | D. | 6 |