题目内容
7.已知an+1-an-3=0,则数列{an}是( )| A. | 等差数列 | B. | 等比数列 | ||
| C. | 摆动数列 | D. | 既等差数列又等比数列 |
分析 将an+1-an-3=0化为:an+1-an=3,利用等差数列的定义判断即可.
解答 解:由题意知,an+1-an-3=0,则an+1-an=3,
∴数列{an}是以3为公差的等差数列,
故选:A.
点评 本题考查了等差数列的定义,属于基础题.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
18.观察下列的规律:$\frac{1}{1},\frac{1}{2},\frac{2}{1}$,$\frac{1}{3},\frac{2}{2},\frac{3}{1}$,$\frac{1}{4},\frac{2}{3},\frac{3}{2},\frac{4}{1}$…则第93个是( )
| A. | $\frac{1}{8}$ | B. | $\frac{2}{13}$ | C. | $\frac{8}{7}$ | D. | $\frac{1}{14}$ |
15.设等差数列{an},{bn}的前n项和分别为Sn,Tn,若$\frac{a_n}{b_n}=\frac{2n-1}{n+1}$,则$\frac{{{S_{11}}}}{{{T_{11}}}}$=( )
| A. | $\frac{7}{4}$ | B. | $\frac{11}{7}$ | C. | 2 | D. | $\frac{7}{2}$ |
2.函数y=$\left\{\begin{array}{l}{3^x},x∈(-∞,1]\\ 3-\frac{3}{x},x∈(1,+∞)\end{array}$的值域为( )
| A. | (0,3) | B. | (0,3] | C. | (0,+∞) | D. | [0,+∞) |
17.在某项测量中,测量结果X服从正态分布N(2,σ2),若X在(0,4)内取值的概率为0.6,则X在(0,2)内取值的概率为( )
| A. | 0.2 | B. | 0.3 | C. | 0.4 | D. | 0.6 |
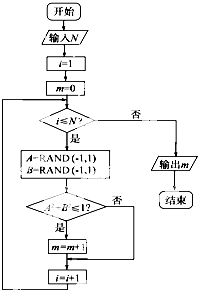 如图所示的程序框图可用来估计π的值(假设函数RAND(-1,1)是产
如图所示的程序框图可用来估计π的值(假设函数RAND(-1,1)是产