题目内容
设函数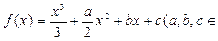 R),函数
R),函数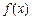 的导数记为
的导数记为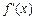 .
.
(1)若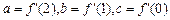 ,求a、b、c的值;
,求a、b、c的值;
(2)在(1)的条件下,记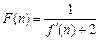 ,求证:F(1)+ F(2)+ F(3)+…+ F(n)<
,求证:F(1)+ F(2)+ F(3)+…+ F(n)<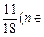 N*);
N*);
(3)设关于x的方程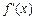 =0的两个实数根为α、β,且1<α<β<2.试问:是否存在正整数n0,使得
=0的两个实数根为α、β,且1<α<β<2.试问:是否存在正整数n0,使得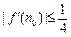 ?说明理由.
?说明理由.
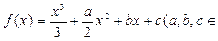 R),函数
R),函数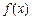 的导数记为
的导数记为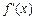 .
.(1)若
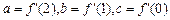 ,求a、b、c的值;
,求a、b、c的值;(2)在(1)的条件下,记
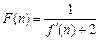 ,求证:F(1)+ F(2)+ F(3)+…+ F(n)<
,求证:F(1)+ F(2)+ F(3)+…+ F(n)<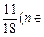 N*);
N*);(3)设关于x的方程
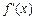 =0的两个实数根为α、β,且1<α<β<2.试问:是否存在正整数n0,使得
=0的两个实数根为α、β,且1<α<β<2.试问:是否存在正整数n0,使得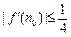 ?说明理由.
?说明理由.略
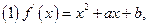 由已知可得
由已知可得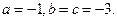 …………4分
…………4分
当n="1" 时,
 <
<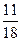 ,
,当n="2" 时,
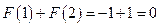 <
< 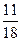 …………7分
…………7分当
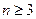 时,
时,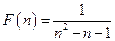 <
<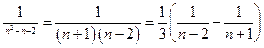
所以F(1)+ F(2)+ F(3)+…+ F(n)< F(1)+F(2)+
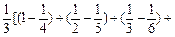 …+
…+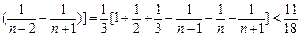 ,
,所以F(1)+ F(2)+ F(3)+…+F(n)<
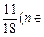 N*). ………………………10分
N*). ………………………10分(3)根据题设,可令
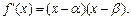
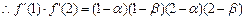
=
 ,
,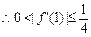 或
或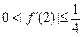 ,所以存在n0=1或2, 使
,所以存在n0=1或2, 使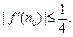 ……14分
……14分
练习册系列答案
相关题目
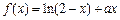 在(0,1)内是增函数.
在(0,1)内是增函数.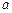 的取值范围;
的取值范围;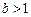 ,求证:
,求证: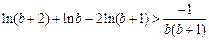 .
.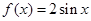 ,则
,则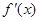 等于( ).
等于( ). 



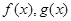 都是定义在R上的函数,且
都是定义在R上的函数,且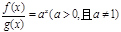 ,
,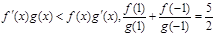 ,则
,则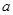 的值为( )
的值为( )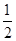
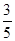
 作曲线
作曲线 的切线,则切线斜率为 .
的切线,则切线斜率为 .
 ,则
,则 ( )
( )


 ,若
,若 在R上可导,则
在R上可导,则 = 。
= 。