题目内容
下列命题为真命题的是( )A.函数y=sin2x-cos2x是奇函数
B.已知命题p:对任意实数x,都有
 <0,则非p可表示为:至少存在一个实数x,使x≤-1,或x≥1
<0,则非p可表示为:至少存在一个实数x,使x≤-1,或x≥1C.“
 >0”是“t2+t-2>0”的必要不充分条件
>0”是“t2+t-2>0”的必要不充分条件D.存在实数m,使2与m-1的等比中项为m
【答案】分析:A.利用奇偶性的定义判断.B.利用全称命题的否定是特称命题判断.C.利用充分条件和必要条件的定义判断.D.利用等比中项的定义判断.
解答:解:A.因为y=sin2x-cos2x=-cos2x,所以为偶函数,所以A错误.
B.因为命题p是全称命题,即p为对任意实数x,都有x2-1<0,即-1<x<1.
所以根据全称命题的否定是特称命题得非p:至少存在一个实数x,使x≤-1,或x≥1,所以B正确.
C.由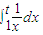 >0得lnt>0,解得t>1.而t2+t-2>0,解得t>1或t<-2.所以“
>0得lnt>0,解得t>1.而t2+t-2>0,解得t>1或t<-2.所以“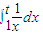 >0”是“t2+t-2>0”的充分不必要条件,所以C错误.
>0”是“t2+t-2>0”的充分不必要条件,所以C错误.
D.若存在实数m,使2与m-1的等比中项为m,则有m2=2(m-1),即m2-2m+2=0,因为△=4-4×2=-4<0,所以方程无解,所以D错误.
故选B.
点评:本题主要考查命题的真假判断.
解答:解:A.因为y=sin2x-cos2x=-cos2x,所以为偶函数,所以A错误.
B.因为命题p是全称命题,即p为对任意实数x,都有x2-1<0,即-1<x<1.
所以根据全称命题的否定是特称命题得非p:至少存在一个实数x,使x≤-1,或x≥1,所以B正确.
C.由
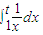 >0得lnt>0,解得t>1.而t2+t-2>0,解得t>1或t<-2.所以“
>0得lnt>0,解得t>1.而t2+t-2>0,解得t>1或t<-2.所以“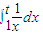 >0”是“t2+t-2>0”的充分不必要条件,所以C错误.
>0”是“t2+t-2>0”的充分不必要条件,所以C错误.D.若存在实数m,使2与m-1的等比中项为m,则有m2=2(m-1),即m2-2m+2=0,因为△=4-4×2=-4<0,所以方程无解,所以D错误.
故选B.
点评:本题主要考查命题的真假判断.

练习册系列答案
相关题目
下列命题为真命题的是( )
| A、?x∈R,x+1>x | B、?x∈Z,x2=2 | C、?x∈R,x2>0 | D、?x∈Z,x2>x |
下列命题为真命题的是( )
| A、a>b是a2>b2的充分条件 | B、|a|>|b|是a2>b2的充要条件 | C、x2=1是x=1的充分条件 | D、α=β是sinα=sinβ的必要不充分条件 |