题目内容

7．设f（x）=x2+11x+7．则f（x+1）=（　　）
A．x2-13x+19B．x2-13x+18C．x2+13x+19D．x2+13x+18

分析 利用代入法，即可求出f（x+1）．

解答 解：∵设f（x）=x2+11x+7，
∴f（x+1）=（x+1）2+11（x+1）+7=x2+13x+19，
故选：C．

点评 本题考查函数的解析式，考查代入法，比较基础．

练习册系列答案
相关题目
17．如图各网格是单位正方形，粗线所表示的图形为某几何体的三视图．则该几何体的体积为（　　）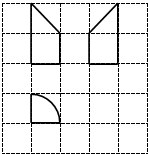
A．$\frac{π}{4}$B．$\frac{π}{3}$C．$\frac{π}{6}$D．$\frac{π}{12}$
18．方程x2-2（m-1）x+3m2=11没有实数根，求m解的集合．
15．函数y=cos（ωx+$\frac{π}{2}$）在[0，$\frac{π}{4}$]上为增函数，则ω的取值范围为（　　）
A．[-2，0）B．[-3，0）C．[-2，2]D．（0，2]
2．若（ax+y）（x-y）6的展开式中x4y3的系数为-35，则a=$\frac{5}{2}$．
12．设函数f（x）=x2-1，那么f[f（x）]=（　　）
A．x4-1B．x4+2x2C．x4+1D．x4-2x2
19．将下列三角函数转化为锐角三角函数，并填在题中横线上：
（1）cos210°=-cos30°；
（2）sin263°42′=-sin83°42′；
（3）cos（-$\frac{π}{6}$）cos$\frac{π}{6}$； 
（4）sin（-$\frac{5}{3}$π）=sin$\frac{π}{3}$；
（5）cos（-$\frac{11}{9}$π）=-cos$\frac{π}{9}$；
（6）cos（-104°26′）=-sin14°26′；
（7）tan632°24′=-tan87°36′；
（8）tan$\frac{17π}{6}$=-tan$\frac{π}{6}$．
4．如果关于x的不等式|x-2|+|x-a|≥a恒成立，则a的最大值是1．
5．已知空间四点A（1，0，0），B（0，1，0），C（0，0，1），P（2，3，m）同在平面α内，则m的值为-4．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网