Question

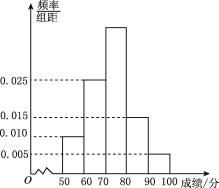
【题目】从2013年开始，国家教育部要求高中阶段每学年都要组织学生进行学生体质健康测试，方案要求以学校为单位组织实施，某校对高一(1)班学生根据《国家学生体质健康标准》的测试项目按百分制进行了预备测试，并对50分以上的成绩进行统计，其频率分布直方图如图.所示，已知[90，100]分数段的人数为2.

(1)求[70，80)分数段的人数；

(2)现根据预备测试成绩从成绩在80分以上(含80分)的学生中任意选出2人代表班级参加学校举行的一项体育比赛，求这2人的成绩一个在[80，90)分数段、一个在[90，100]分数段的概率．

Answer 1

【答案】（1）18；（2）

【解析】

⑴由频率分布直方图可知，各个分数段的频率，求出分以上的总人数，分数段的频率，即可求出人数

⑵求得分数段的人数，列举出所有可能性情况，然后计算结果

(1)由频率分布直方图可知，[90，100]分数段的频率为0.005×10＝0.05，

[70，80)分数段的频率为1－(0.010＋0.025＋0.015＋0.005)×10＝0.45，

因为[90，100]分数段的人数为2，所以50分以上的总人数为＝40，

所以[70，80)分数段的人数为40×0.45＝18.

(2)由(1)可求得[80，90)分数段的人数为40×0.15＝6，

设[80，90)分数段的6名学生分别为A1，A2，A3，A4，A5，A6，[90，100]分数段的2名学生分别为B1，B2，

则从中选出2人的选法有(A1，A2)，(A1，A3)，(A1，A4)，(A1，A5)，(A1，A6)，(A1，B1)，(A1，B2)，(A2，A3)，(A2，A4)，(A2，A5)，(A2，A6)，(A2，B1)，(A2，B2)，(A3，A4)，(A3，A5)，(A3，A6)，(A3，B1)，(A3，B2)，(A4，A5)，(A4，A6)，(A4，B1)，(A4，B2)，(A5，A6)，(A5，B1)，(A5，B2)，(A6，B1)，(A6，B2)，(B1，B2)，共28种.

其中这2人的成绩一个在[80，90)分数段、一个在[90，100]分数段的情况有(A1，B1)，(A1，B2)，(A2，B1)，(A2，B2)，(A3，B1)，(A3，B2)，(A4，B1)，(A4，B2)，(A5，B1)，(A5，B2)，(A6，B1)，(A6，B2)，共12种，

则所求概率P＝＝.