题目内容
【题目】已知F1、F2是椭圆C的左右焦点,点A,B为其左右顶点,P为椭圆C上(异于A、B)的一动点,当P点坐标为(1, ![]() )时,△PF1F2的面积为
)时,△PF1F2的面积为 ![]() ,分别过点A、B、P作椭圆C的切线l1 , l2 , l,直线l与l1 , l2分别交于点R,T.
,分别过点A、B、P作椭圆C的切线l1 , l2 , l,直线l与l1 , l2分别交于点R,T. 
(1)求椭圆C的方程;
(2)(i)求证:以RT为直径的圆过定点,并求出定点M的坐标;
(ii)求△RTM的面积最小值.
【答案】
(1)解:∵F1、F2是椭圆C的左右焦点,点A,B为其左右顶点,
P为椭圆C上(异于A、B)的一动点,当P点坐标为(1, ![]() )时,△PF1F2的面积为
)时,△PF1F2的面积为 ![]() ,
,
∴ ![]() =
= ![]() ,解得c=1,
,解得c=1,
又∵2a=|PF1|+|PF2|=4,∴a=2,b= ![]() ,
,
故椭圆C的方程为 ![]() .
.
(2)证明:(i)由题意直线l的斜率存在,设直线l为:y=kx+m,
联立 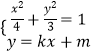 ,得(3+4k2)x2+8kmx+4m2﹣12=0,
,得(3+4k2)x2+8kmx+4m2﹣12=0,
△=64k2m2﹣4(3+4k2)(4m2﹣12)=0,
化简,得m2=3+4k2,
R(﹣2,﹣2k+m),T(2,2k+m),
由对称性,知定点M在x轴上,
设M(x,0),M在RT为直线的圆上,∴MR⊥MT,
∴ ![]() =(﹣2﹣x)(2﹣x)+(﹣2k+m)(2k+m)=x2﹣4+m2﹣4k2=0,
=(﹣2﹣x)(2﹣x)+(﹣2k+m)(2k+m)=x2﹣4+m2﹣4k2=0,
解得x=±1,
∴定点M即为左右焦点F1,F2,其坐标为(±1,0).
解:(ii)由图形的对称性,不妨取M为右焦点F2(1,0),
点P在x轴上方,
S△RTM=S四边形ABTR﹣S△BDA=2(m+k),
令m+k=t,则m=t﹣k,代入m2=3+4k2,
得3k2+2tk+3﹣t2=0,
△=4(4t2﹣9)≥0,
∵t>0,∴t≥ ![]() ,S△RDA≥3,
,S△RDA≥3,
当m=2,k=﹣ ![]() 时,取等号,
时,取等号,
故△RTM的面积的最小值为3.
【解析】(1)由当P点坐标为(1, ![]() )时,△PF1F2的面积为
)时,△PF1F2的面积为 ![]() ,求出c=1,2a=|PF1|+|PF2|=4,由此能求出椭圆C的方程.(2)(i)设直线l为:y=kx+m,与椭圆联立,得(3+4k2)x2+8kmx+4m2﹣12=0,由此利用根的判别式、椭圆对称性,向量数量积,结合已知条件能证明以RT为直径的圆过定点,并求出定点M的坐标.(ii)由图形的对称性,取M为右焦点F2(1,0),S△RTM=S四边形ABTR﹣S△BDA=2(m+k),由此能求出△RTM的面积的最小值为3.
,求出c=1,2a=|PF1|+|PF2|=4,由此能求出椭圆C的方程.(2)(i)设直线l为:y=kx+m,与椭圆联立,得(3+4k2)x2+8kmx+4m2﹣12=0,由此利用根的判别式、椭圆对称性,向量数量积,结合已知条件能证明以RT为直径的圆过定点,并求出定点M的坐标.(ii)由图形的对称性,取M为右焦点F2(1,0),S△RTM=S四边形ABTR﹣S△BDA=2(m+k),由此能求出△RTM的面积的最小值为3.

 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案【题目】某中学调查了某班全部45名同学参加书法社团和演讲社团的情况,数据如下表:(单位:人)
参加书法社团 | 未参加书法社团 | |
参加演讲社团 | 8 | 5 |
未参加演讲社团 | 2 | 30 |
(1)从该班随机选1名同学,求该同学至少参加一个社团的概率;
(2)在既参加书法社团又参加演讲社团的8名同学中,有5名男同学A1,A2,A3,A4,A5,3名女同学B1,B2,B3.现从这5名男同学和3名女同学中各随机选1人,求A1被选中且B1未被选中的概率.
【题目】某险种的基本保费为a(单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下:
上年度出险次数 | 0 | 1 | 2 | 3 | 4 | ≥5 |
保费 | 0.85a | a | 1.25a | 1.5a | 1.75a | 2a |
随机调查了该险种的200名续保人在一年内的出险情况,得到如下统计表:
出险次数 | 0 | 1 | 2 | 3 | 4 | ≥5 |
频数 | 60 | 50 | 30 | 30 | 20 | 10 |
(1)记A为事件:“一续保人本年度的保费不高于基本保费”,求P(A)的估计值;
(2)记B为事件:“一续保人本年度的保费高于基本保费但不高于基本保费的160%”,求P(B)的估计值;
(3)求续保人本年度平均保费的估计值.