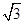题目内容
已知|
|=1,|
|=2,
•
=1,若
-
与
-
的夹角为60°,则|
|的最大值为( )
| a |
| b |
| a |
| b |
| a |
| c |
| b |
| c |
| c |
A.
| B.
| C.
| D.
|
|
|=1,|
|=2,
•
=|
||
|cos<
,
>=1,
∴cos<
,
>=
,∴<
,
>=
,设
=
,
=
,
=
,
以∠AOB的角平分线为x轴,O为坐标原点建立平面直角坐标系,
则A(
,
),B(
,-1),设C(x,y),
cos<
-
,
-
>=
=
,
整理得(x-
)2+y2=1,∴C点的轨迹为圆,圆心坐标为(
,0),
∴|
|=
,其最大值为1+
.
故选:D.
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
∴cos<
| a |
| b |
| 1 |
| 2 |
| a |
| b |
| π |
| 3 |
| a |
| OA |
| b |
| OB |
| c |
| OC |
以∠AOB的角平分线为x轴,O为坐标原点建立平面直角坐标系,
则A(
| ||
| 2 |
| 1 |
| 2 |
| 3 |
cos<
| a |
| c |
| b |
| c |
(x-
| ||||||||||||
|
| 1 |
| 2 |
整理得(x-
| 3 |
| 3 |
∴|
| c |
| x2+y2 |
| 3 |
故选:D.

练习册系列答案
相关题目
 中,
中, ,
, ,
,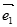 =
=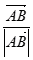 ,
,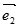 =
=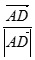 ,
,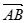 与
与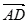 的夹角为
的夹角为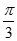 .
.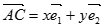 ,求
,求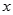 、
、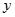 的值;
的值;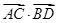 的值;
的值;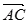 与
与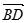 的夹角的余弦值.
的夹角的余弦值.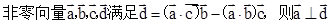
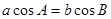 ,则△ABC是等腰三角形
,则△ABC是等腰三角形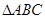 中,
中,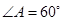 ,边长a,c分别为a=4,c=
,边长a,c分别为a=4,c=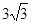 ,则
,则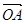 +x
+x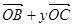 ,且A.B.C三点共线,求
,且A.B.C三点共线,求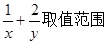 .
.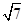 ,〈a,b〉=
,〈a,b〉=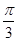 ,则|b|=( )
,则|b|=( )