题目内容
【题目】已知圆C：x2﹣（1+a）x+y2﹣ay+a=0（a∈R）． （Ⅰ） 若a=1，求直线y=x被圆C所截得的弦长；
（Ⅱ） 若a＞1，如图，圆C与x轴相交于两点M，N（点M在点N的左侧）．过点M的动直线l与圆O：x2+y2=4相交于A，B两点．问：是否存在实数a，使得对任意的直线l均有∠ANM=∠BNM？若存在，求出实数a的值，若不存在，请说明理由．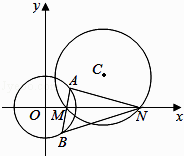
【答案】解：（Ⅰ） 当a=1时，圆C：x2﹣2x+y2﹣y+1=0， 圆心C（1， 
），半径r= 
= ，
圆心C（1， ）到直线y=x的距离d= 
= 
，
∴直线y=x被圆C所截得的弦长为：2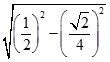 
= 
．
（Ⅱ）令y=0，得x2﹣（1+a）x+a=0，即（x﹣1）（x﹣a）=0，解得x=1，或x=a，
∴M（1，0），N（a，0）．
假设存在实数a，当直线AB与x轴不垂直时，设直线AB的方程为y=k（x﹣1），
代入x2+y2=4得，（1+k2）x2﹣2k2x+k2﹣4=0，
设A（x1 ， y1），B（x2 ， y2），从而 
，x1x2= 
．
∵NA、NB的斜率之和为 
+ 
= 
，
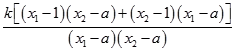而（x1﹣1）（x2﹣a）+（x2﹣1）（x1﹣a）
=2x1x2﹣（a+1）（x2+x1）+2a= 
+2a= 
，
∵∠ANM=∠BNM，所以，NA、NB的斜率互为相反数， 
=0，即 =0，得a=4．
当直线AB与x轴垂直时，仍然满足∠ANM=∠BNM，即NA、NB的斜率互为相反数．
综上，存在a=4，使得∠ANM=∠BNM
【解析】（Ⅰ）当a=1时，求出圆心C（1， 
），半径r= ，求出圆心C到直线y=x的距离，由此利用勾股定理能求出直线y=x被圆C所截得的弦长．（Ⅱ）先求出所以M（1，0），N（a，0），假设存在实数a，当直线AB与x轴不垂直时，设直线AB的方程为y=k（x﹣1），代入x2+y2=4，利用韦达定理，根据NA、NB的斜率之和等于零求得a的值．经过检验，当直线AB与x轴垂直时，这个a值仍然满足∠ANM=∠BNM，从而得出结论．
