题目内容
7. 如图,△ABC内接于⊙O,AE与⊙O相切于点A,BD平分∠ABC,交⊙O于点D,交AE的延长线于点E,DF⊥AE于点F.
如图,△ABC内接于⊙O,AE与⊙O相切于点A,BD平分∠ABC,交⊙O于点D,交AE的延长线于点E,DF⊥AE于点F.(Ⅰ)求证:$\frac{AB}{AD}$=$\frac{AE}{DE}$;
(Ⅱ)求证:AC=2AF.
分析 (Ⅰ)证明△DAE∽△ABE,即可证明$\frac{AB}{AD}$=$\frac{AE}{DE}$;
(Ⅱ)过点D作DH⊥AC,垂足为H,连接CD,证明DF=DH,AH=CH,即可证明AC=2AF.
解答 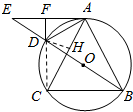 证明:(Ⅰ)∵AE与⊙O相切于点A,∴∠EAD=∠EBA,
证明:(Ⅰ)∵AE与⊙O相切于点A,∴∠EAD=∠EBA,
∵∠E=∠E,
∴△DAE∽△ABE,
∴$\frac{AB}{AD}$=$\frac{AE}{DE}$;
(Ⅱ)过点D作DH⊥AC,垂足为H,连接CD,则:
∵∠EAD=∠ABD,∠DAC=∠DBC,BD平分∠ABC,
∴∠EAD=∠DAC
∵DF⊥AB,DH⊥AC,
∴DF=DH
在Rt△DFA和Rt△DHA中,DF=DH,DA=DA,
∴Rt△DFA≌Rt△DHA,
∴AF=AH,
∵∠ABD=∠CBD,
∴DC=DA,
∵DH⊥AC,
∴AH=CH,
∴AC=2AH=2AF.
点评 本题考查三角形相似的判定与性质,考查三角形全等的证明,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
19.在等比数列{an}中,a3=4,a7=12,则a11=( )
| A. | 16 | B. | 18 | C. | 36 | D. | 48 |
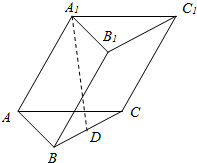 如图,斜三棱柱ABC-A1B1C1的底面是边长为4的正三角形,D是BC的中点,A1D⊥平面ABC.
如图,斜三棱柱ABC-A1B1C1的底面是边长为4的正三角形,D是BC的中点,A1D⊥平面ABC.