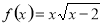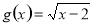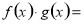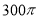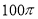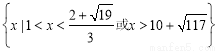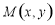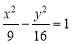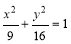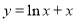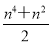题目内容
设椭圆的方程为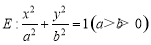 ,斜率为1的直线不经过原点
,斜率为1的直线不经过原点 ,而且与椭圆相交于
,而且与椭圆相交于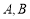 两点,
两点,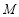 为线段
为线段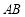 的中点.
的中点.
(1)问:直线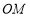 与
与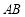 能否垂直?若能,求
能否垂直?若能,求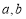 之间满足的关系式;若不能,说明理由;
之间满足的关系式;若不能,说明理由;
(2)已知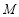 为
为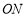 的中点,且
的中点,且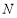 点在椭圆上.若
点在椭圆上.若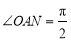 ,求
,求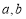 之间满足的关系式.
之间满足的关系式.
(1)直线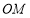 与
与 不能垂直;(2)
不能垂直;(2)
【解析】
试题分析:(1)设直线 的方程为
的方程为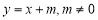 ,与椭圆方程联立,消去
,与椭圆方程联立,消去 整理为关于
整理为关于 的一元二次方程,因为有两个交点则判别式应大于0,由韦达定理可得根与系数的关系,用中点坐标公式求点
的一元二次方程,因为有两个交点则判别式应大于0,由韦达定理可得根与系数的关系,用中点坐标公式求点 的坐标。求出直线
的坐标。求出直线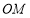 的斜率,假设两直线垂直则斜率相乘等于
的斜率,假设两直线垂直则斜率相乘等于 ,解出
,解出 的关系式,根据关系式及椭圆中
的关系式,根据关系式及椭圆中 的关系判断假设成立与否。(2)∵M为ON的中点,M为AB的中点,∴四边形OANB为平行四边形.
的关系判断假设成立与否。(2)∵M为ON的中点,M为AB的中点,∴四边形OANB为平行四边形.
∵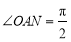 ,∴四边形OANB为矩形,∴
,∴四边形OANB为矩形,∴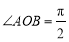 ,转化为向量问题,可得
,转化为向量问题,可得 的关系式。由中点坐标公式可得点
的关系式。由中点坐标公式可得点 的坐标,将其代入椭圆方程,与上式联立消去
的坐标,将其代入椭圆方程,与上式联立消去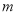 即可得
即可得 之间满足的关系式。
之间满足的关系式。
试题解析:解答:(1)∵斜率为1的直线不经过原点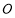 ,而且与椭圆相交于
,而且与椭圆相交于 两点,
两点,
∴可以设直线 的方程为
的方程为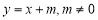 .
.
∵ ,∴
,∴ ,
,
∴ . ① 1分
. ① 1分
∵直线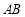 与椭圆相交于
与椭圆相交于 两点,∴
两点,∴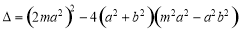

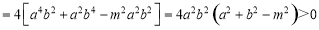 . ② 2分
. ② 2分
且 . ③ 3分
. ③ 3分
∵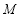 为线段
为线段 的中点,∴
的中点,∴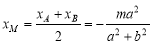 ,
,
∴ ,∴
,∴ . 4分
. 4分
假设直线 与
与 能垂直.
能垂直.
∵直线 的斜率为1,∴直线
的斜率为1,∴直线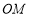 的斜率为-1,
的斜率为-1,
∴ ,∴
,∴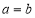 . 5分
. 5分
∵在椭圆方程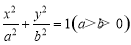 中,
中, ,
,
∴假设不正确,在椭圆中直线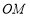 与
与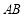 不能垂直. 6分
不能垂直. 6分
(2)∵M为ON的中点,M为AB的中点,∴四边形OANB为平行四边形.
∵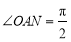 ,∴四边形OANB为矩形,∴
,∴四边形OANB为矩形,∴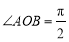 , 8分
, 8分
∴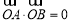 ,∴
,∴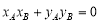 ,∴
,∴ ,
,
∴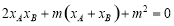 ,
,
∴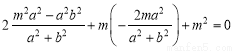 ,整理得
,整理得 . 10分
. 10分
∵ 点在椭圆上,∴
点在椭圆上,∴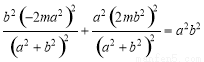 ,
,
∴ . 此时
. 此时 ,满足
,满足 ,
,
消去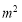 得
得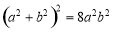 ,即
,即 . 12分
. 12分
考点:1直线与椭圆的位置关系;2直线垂直时斜率的关系;3转化思想。