题目内容
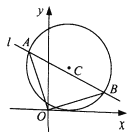
【题目】己知点![]() ,直线l与圆C:(x一1)2+(y一2)2=4相交于A,B两点,且OA⊥OB.
,直线l与圆C:(x一1)2+(y一2)2=4相交于A,B两点,且OA⊥OB.

(1)若直线OA的方程为y=一3x,求直线OB被圆C截得的弦长;
(2)若直线l过点(0,2),求l的方程.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)根据题意,求得直线OB的方程![]() ,利用点到直线的距离公式求得圆心
,利用点到直线的距离公式求得圆心![]() 到直线OB的距离,之后应用圆中的特殊三角形,求得弦长;
到直线OB的距离,之后应用圆中的特殊三角形,求得弦长;
(2)根据题意,可判断直线的斜率是存在的,设出其方程,与圆的方程联立,得到两根和与两根积,根据OA⊥OB,利用向量数量积等于零得到![]() 所满足的等量关系式,求得结果.
所满足的等量关系式,求得结果.
(1)因为直线OA的方程为![]() ,
,![]() ,
,
所以直线OB的方程![]() .
.
从而圆心![]() 到直线OB的距离为:
到直线OB的距离为: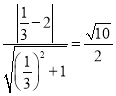
所以直线OB被团C截得的弦长为: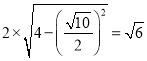 .
.
(2)依题意,直线l的斜率必存在,不妨设其为k,则l的方程为![]() ,
,
又设![]() ,
,![]() .
.
由![]() 得
得![]() ,
,
所以![]() ,
,![]() .
.
从而![]() .
.
所以![]() .
.
因为![]() ,所以
,所以![]() ,即
,即![]() ,解得
,解得![]() .
.
所以l的方程为![]() .
.

 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案【题目】一个工厂在某年连续10个月每月产品的总成本y(万元)与该月产量x(万件)之间有如下一组数据:
x | 1.08 | 1.12 | 1.19 | 1.28 | 1.36 | 1.48 | 1.59 | 1.68 | 1.80 | 1.87 |
y | 2.25 | 2.37 | 2.40 | 2.55 | 2.64 | 2.75 | 2.92 | 3.03 | 3.14 | 3.26 |
(1)通过画散点图,发现可用线性回归模型拟合y与x的关系,请用相关系数加以说明;
(2)①建立月总成本y与月产量x之间的回归方程;
②通过建立的y关于x的回归方程,估计某月产量为1.98万件时,此时产品的总成本为多少万元?
(均精确到0.001)
附注:①参考数据:![]() ,
,
![]() ,
,
②参考公式:相关系数 ,
,
回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: .
.
【题目】某中学一名数学老师对全班50名学生某次考试成绩分男女生进行统计(满分150分),其中120分(含120分)以上为优秀,绘制了如图所示的两个频率分布直方图:

(1)根据以上两个直方图完成下面的![]() 列联表:
列联表:
性别 成绩 | 优秀 | 不优秀 | 总计 |
男生 | |||
女生 | |||
总计 |
(2)根据(1)中表格的数据计算,你有多大把握认为学生的数学成绩与性别之间有关系?
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
附:![]() ,其中
,其中![]() .
.

