题目内容
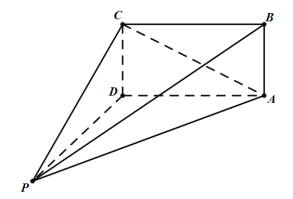
【题目】某生态农场有一矩形地块,地块内有一半圆形池塘(如图所示),其中![]() 百米,
百米,![]() 百米,半圆形池塘的半径为1百米,圆心
百米,半圆形池塘的半径为1百米,圆心![]() 与线段
与线段![]() 的中点重合,半圆与
的中点重合,半圆与![]() 的左侧交点为
的左侧交点为![]() .该农场计划分别在
.该农场计划分别在![]() 和
和![]() 上各选一点
上各选一点![]() ,修建道路
,修建道路![]() ,要求
,要求![]() 与半圆相切.
与半圆相切.
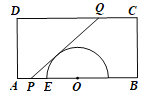
(1)若![]() ,求该道路的总长;
,求该道路的总长;
(2)若![]() 为观光道路,修建费用是4万元/百米,
为观光道路,修建费用是4万元/百米,![]() 为便道,修建费用是1万元/百米,求修建观光道路与便道的总费用的最小值.
为便道,修建费用是1万元/百米,求修建观光道路与便道的总费用的最小值.
【答案】(1)![]() 百米;(2)
百米;(2)![]() 万元.
万元.
【解析】
(1)利用图中边角关系,分别计算出![]() ,
,![]() 的长度,相加即可;
的长度,相加即可;
(2)设![]() ,得
,得![]() 的取值范围是
的取值范围是![]() ,可得修建观光道路与便道的总费用
,可得修建观光道路与便道的总费用![]() ,利用导数求其最值即可.
,利用导数求其最值即可.
(1)因为![]() ,所以
,所以![]() .
.
而![]() ,
,
所以![]() .
.
答:道路的总长为![]() 百米.
百米.
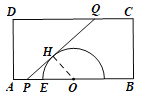
(2)设![]() .
.
若点![]() 与点
与点![]() 重合,则
重合,则![]() ;
;
若点![]() 与点
与点![]() 重合,则
重合,则![]() ,
,
所以由题意,![]() 的取值范围是
的取值范围是![]() .
.
设切点为![]() ,连结
,连结![]() .
.
则![]() .
.
设修建观光道路与便道的总费用为![]() 万元,则
万元,则![]()
![]() .
.
设![]() ,
,
则![]() .
.
令![]() ,得
,得![]() ,令
,令![]() ,且
,且![]() .
.
列表如下:
|
|
|
|
| - | 0 | + |
| ↘ | 极小值 | ↗ |
所以当![]() 时,
时,![]() 取得最小值.
取得最小值.
所以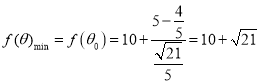 .
.
答:修建观光道路与便道的总费用的最小值为![]() 万元.
万元.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
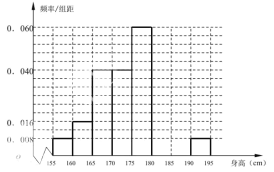
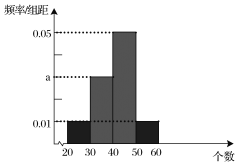
【题目】为了了解某学校高二年级学生的物理成绩,从中抽取![]() 名学生的物理成绩(百分制)作为样本,按成绩分成5组:
名学生的物理成绩(百分制)作为样本,按成绩分成5组:![]() ,频率分布直方图如图所示,成绩落在
,频率分布直方图如图所示,成绩落在![]() 中的人数为20.
中的人数为20.

男生 | 女生 | 合计 | |
优秀 | |||
不优秀 | |||
合计 |
(1)求![]() 和
和![]() 的值;
的值;
(2)根据样本估计总体的思想,估计该校高二学生物理成绩的平均数![]() 和中位数
和中位数![]() ;
;
(3)成绩在80分以上(含80分)为优秀,样本中成绩落在![]() 中的男、女生人数比为1:2,成绩落在
中的男、女生人数比为1:2,成绩落在![]() 中的男、女生人数比为3:2,完成
中的男、女生人数比为3:2,完成![]() 列联表,并判断是否所有95%的把握认为物理成绩优秀与性别有关.
列联表,并判断是否所有95%的把握认为物理成绩优秀与性别有关.
参考公式和数据:
| 0.50 | 0.05 | 0.025 | 0.005 |
| 0.455 | 3.841 | 5.024 | 7.879 |