题目内容
已知数列{2n-1·an}的前n项和Sn=1-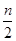 .
.
(1)求数列{an}的通项公式;
(2)设bn=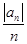 ,求数列
,求数列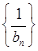 的前n项和.
的前n项和.
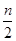 .
.(1)求数列{an}的通项公式;
(2)设bn=
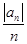 ,求数列
,求数列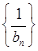 的前n项和.
的前n项和.(1)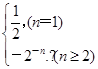 (2)(1-n)·2n+1-2
(2)(1-n)·2n+1-2
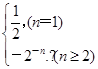 (2)(1-n)·2n+1-2
(2)(1-n)·2n+1-2(1)由题意可知:Sn-1=1-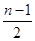 (n≥2),
(n≥2),
又2n-1·an=Sn-Sn-1,∴2n-1·an=-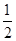 .
.
∴an=-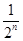 =-2-n(n≥2).∴a1=-
=-2-n(n≥2).∴a1=-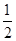 .
.
又S1=1-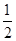 =
=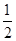 ,∴a1≠S1,∴an=
,∴a1≠S1,∴an=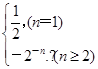
(2)由题意知bn=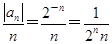 (n≥2),∴
(n≥2),∴ =n·2n(n≥2).
=n·2n(n≥2).
∵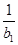 =
=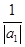 =2,∴
=2,∴ =n·2n(n≥1).
=n·2n(n≥1).
设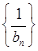 的前n项和为
的前n项和为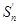 ,则
,则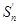 =1×2+2×22+3×23+…+n·2n,
=1×2+2×22+3×23+…+n·2n,
2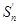 =1×22+2×23+3×24+…+(n-1)·2n+n·2n+1,
=1×22+2×23+3×24+…+(n-1)·2n+n·2n+1,
∴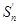 -2
-2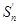 =1×2+22+23+…+2n-n·2n+1=2+22+…+2n-n·2n+1,
=1×2+22+23+…+2n-n·2n+1=2+22+…+2n-n·2n+1,
∴-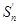 =(1-n)·2n+1-2,∴
=(1-n)·2n+1-2,∴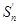 =(n-1)·2n+1+2
=(n-1)·2n+1+2
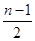 (n≥2),
(n≥2),又2n-1·an=Sn-Sn-1,∴2n-1·an=-
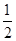 .
.∴an=-
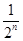 =-2-n(n≥2).∴a1=-
=-2-n(n≥2).∴a1=-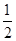 .
.又S1=1-
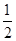 =
=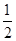 ,∴a1≠S1,∴an=
,∴a1≠S1,∴an=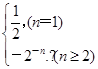
(2)由题意知bn=
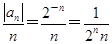 (n≥2),∴
(n≥2),∴ =n·2n(n≥2).
=n·2n(n≥2).∵
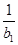 =
=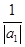 =2,∴
=2,∴ =n·2n(n≥1).
=n·2n(n≥1).设
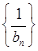 的前n项和为
的前n项和为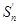 ,则
,则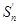 =1×2+2×22+3×23+…+n·2n,
=1×2+2×22+3×23+…+n·2n,2
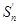 =1×22+2×23+3×24+…+(n-1)·2n+n·2n+1,
=1×22+2×23+3×24+…+(n-1)·2n+n·2n+1,∴
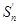 -2
-2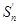 =1×2+22+23+…+2n-n·2n+1=2+22+…+2n-n·2n+1,
=1×2+22+23+…+2n-n·2n+1=2+22+…+2n-n·2n+1,∴-
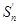 =(1-n)·2n+1-2,∴
=(1-n)·2n+1-2,∴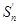 =(n-1)·2n+1+2
=(n-1)·2n+1+2
练习册系列答案
相关题目
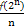 (n∈N*),bn=
(n∈N*),bn=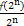 (n∈N*).
(n∈N*).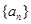 的通项公式为
的通项公式为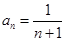 ,前
,前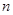 项和为
项和为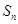 ,若对任意的正整数
,若对任意的正整数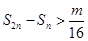 恒成立,则常数
恒成立,则常数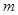 所能取得的最大整数为 .
所能取得的最大整数为 .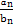 }的前n项和Sn.
}的前n项和Sn. ,
, ,-
,- ,
,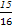 ,…的一个通项公式可以是 .
,…的一个通项公式可以是 .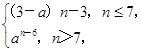 且数列{an}是递增数列,则实数a的范围是__________.
且数列{an}是递增数列,则实数a的范围是__________.