题目内容
已知函数f(x)是定义在R上不恒为零的函数,且对于任意实数a,b∈R,满足:f(a·b)=af(b)+bf(a),f(2)=2,an=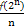 (n∈N*),bn=
(n∈N*),bn=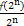 (n∈N*).
(n∈N*).
考察下列结论:
①f(0)=f(1);②f(x)为偶函数;
③数列{an}为等比数列;
④数列{bn}为等差数列.
其中正确的结论共有( )
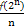 (n∈N*),bn=
(n∈N*),bn=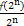 (n∈N*).
(n∈N*).考察下列结论:
①f(0)=f(1);②f(x)为偶函数;
③数列{an}为等比数列;
④数列{bn}为等差数列.
其中正确的结论共有( )
| A.1个 | B.2个 | C.3个 | D.4个 |
C
根据所给的四个条件,逐条验证即可.注意②中用特殊值验证,③④用定义判断.
∵f(0)=f(0×0)=0,
f(1)=f(1×1)=2f(1),
∴f(1)=0,①正确;
又f(1)=f((-1)×(-1))=-2f(-1),
∴f(-1)=0,f(-2)=f(-1×2)=-f(2)+2f(-1)=-2≠f(2),
故f(x)不是偶函数,故②错;
∵f(2n)=f(2·2n-1)=2f(2n-1)+2n-1f(2)=2f(2n-1)+2n,
∴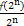 =
=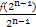 +1,
+1,
即bn=bn-1+1,
∴{bn}是等差数列,④正确;
b1=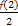 =1,
=1,
bn=1+(n-1)·1=n,
f(2n)=2nbn=n·2n,
an=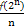 =2n,
=2n,
故数列{an}是等比数列,③正确.故选C.
∵f(0)=f(0×0)=0,
f(1)=f(1×1)=2f(1),
∴f(1)=0,①正确;
又f(1)=f((-1)×(-1))=-2f(-1),
∴f(-1)=0,f(-2)=f(-1×2)=-f(2)+2f(-1)=-2≠f(2),
故f(x)不是偶函数,故②错;
∵f(2n)=f(2·2n-1)=2f(2n-1)+2n-1f(2)=2f(2n-1)+2n,
∴
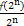 =
=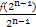 +1,
+1,即bn=bn-1+1,
∴{bn}是等差数列,④正确;
b1=
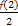 =1,
=1,bn=1+(n-1)·1=n,
f(2n)=2nbn=n·2n,
an=
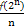 =2n,
=2n,故数列{an}是等比数列,③正确.故选C.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
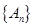 满足
满足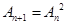 ,则称数列
,则称数列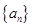 中,
中,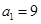 ,点
,点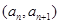 在函数
在函数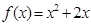 的图象上,其中
的图象上,其中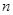 为正整数.
为正整数.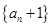 是“平方递推数列”,且数列
是“平方递推数列”,且数列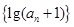 为等比数列;
为等比数列;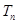 ,
,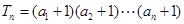 ,求
,求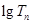 ;
;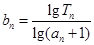 ,求数列
,求数列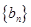 的前
的前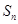 ,并求使
,并求使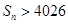 的
的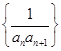 的前n项和,若Tn≤
的前n项和,若Tn≤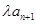 ¨对
¨对 恒成立,求实数
恒成立,求实数 的最小值.
的最小值.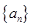 的首项为
的首项为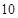 ,公差为
,公差为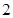 ,等比数列
,等比数列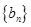 的首项为
的首项为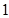 ,公比为
,公比为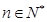 .
.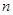 个正方形的边长为
个正方形的边长为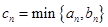 ,求前
,求前 .
.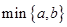 表示
表示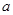 与
与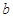 的最小值.)
的最小值.)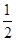 ,an,Sn成等差数列.
,an,Sn成等差数列.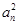 =
=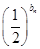 ,设cn=
,设cn=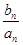 ,求数列{cn}的前n项和Tn.
,求数列{cn}的前n项和Tn.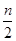 .
.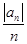 ,求数列
,求数列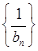 的前n项和.
的前n项和.