题目内容
某联欢晚会举行抽奖活动,举办方设置了甲.乙两种抽奖方案,方案甲的中奖率为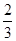 ,中将可以获得2分;方案乙的中奖率为
,中将可以获得2分;方案乙的中奖率为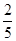 ,中将可以得3分;未中奖则不得分.每人有且只有一次抽奖机会,每次抽奖中将与否互不影响,晚会结束后凭分数兑换奖品.
,中将可以得3分;未中奖则不得分.每人有且只有一次抽奖机会,每次抽奖中将与否互不影响,晚会结束后凭分数兑换奖品.
(1)若小明选择方案甲抽奖,小红选择方案乙抽奖,记他们的累计得分为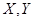 ,求
,求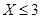 的概率;
的概率;
(2)若小明.小红两人都选择方案甲或方案乙进行抽奖,问:他们选择何种方案抽奖,累计的得分的数学期望较大?
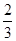 ,中将可以获得2分;方案乙的中奖率为
,中将可以获得2分;方案乙的中奖率为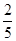 ,中将可以得3分;未中奖则不得分.每人有且只有一次抽奖机会,每次抽奖中将与否互不影响,晚会结束后凭分数兑换奖品.
,中将可以得3分;未中奖则不得分.每人有且只有一次抽奖机会,每次抽奖中将与否互不影响,晚会结束后凭分数兑换奖品.(1)若小明选择方案甲抽奖,小红选择方案乙抽奖,记他们的累计得分为
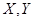 ,求
,求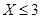 的概率;
的概率;(2)若小明.小红两人都选择方案甲或方案乙进行抽奖,问:他们选择何种方案抽奖,累计的得分的数学期望较大?
(1)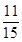
(2)选择方案甲进行抽奖时,累计得分的数学期望最大
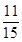
(2)选择方案甲进行抽奖时,累计得分的数学期望最大
试题分析:解:(Ⅰ)由已知得:小明中奖的概率为
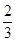 ,小红中奖的概率为
,小红中奖的概率为 ,两人中奖与否互不影响,
,两人中奖与否互不影响,记“这2人的累计得分
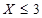 ”的事件为A,则A事件的对立事件为“
”的事件为A,则A事件的对立事件为“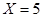 ”,
”, 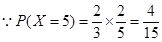 ,
,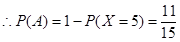
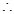 这两人的累计得分
这两人的累计得分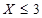 的概率为
的概率为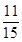 . 6分
. 6分(Ⅱ)设小明.小红都选择方案甲抽奖中奖的次数为
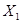 ,都选择方案乙抽奖中奖的次数为
,都选择方案乙抽奖中奖的次数为 ,则这两人选择方案甲抽奖累计得分的数学期望为
,则这两人选择方案甲抽奖累计得分的数学期望为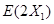 ,选择方案乙抽奖累计得分的数学期望为
,选择方案乙抽奖累计得分的数学期望为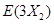
由已知:
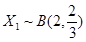 ,
,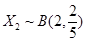
 ,
,
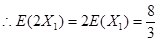 ,
,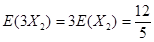
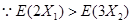
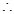 他们都在选择方案甲进行抽奖时,累计得分的数学期望最大. 12分
他们都在选择方案甲进行抽奖时,累计得分的数学期望最大. 12分点评:主要是考查了独立事件的概率以及期望值的运用,属于中档题。

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案
相关题目
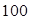 个大小相同的红球、白球和黑球,其中有
个大小相同的红球、白球和黑球,其中有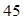 个红球,从中摸出
个红球,从中摸出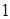 个球,若摸出白球的概率为
个球,若摸出白球的概率为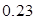 ,则摸出黑球的概率为____________.
,则摸出黑球的概率为____________.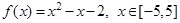 ,若从区间
,若从区间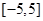 内随机选取一个实数
内随机选取一个实数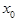 ,则所选取的实数
,则所选取的实数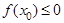 的概率为( )
的概率为( )  、
、 、
、 、
、 四个小球的抽奖箱中同时抽出两个小球,两个小球号码相加之和等于
四个小球的抽奖箱中同时抽出两个小球,两个小球号码相加之和等于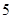 中一等奖,等于
中一等奖,等于 中二等奖,等于
中二等奖,等于 .已知该足球队进行一场比赛得分的期望是1, 则
.已知该足球队进行一场比赛得分的期望是1, 则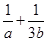 的最小值为( )
的最小值为( )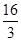
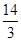
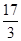
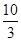
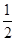 ,各局比赛的结束相互独立,第1局甲当裁判.
,各局比赛的结束相互独立,第1局甲当裁判.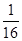
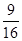
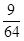
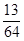
 ,
,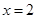 时,
时,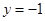 .
.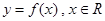 单调递增,则
单调递增,则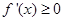 .
.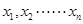 的平均值为
的平均值为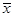 ,方差为
,方差为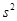 ,则
,则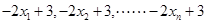 的平均值为
的平均值为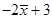 ,方差为
,方差为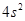 .
.