题目内容
甲、乙、丙三人进行羽毛球练习赛,其中两人比赛,另一人当裁判,每局比赛结束时,负的一方在下一局当裁判.设各局中双方获胜的概率均为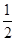 ,各局比赛的结束相互独立,第1局甲当裁判.
,各局比赛的结束相互独立,第1局甲当裁判.
(Ⅰ)求第4局甲当裁判的概率;
(Ⅱ)X表示前4局中乙当裁判的次数,求X的数学期望.
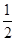 ,各局比赛的结束相互独立,第1局甲当裁判.
,各局比赛的结束相互独立,第1局甲当裁判.(Ⅰ)求第4局甲当裁判的概率;
(Ⅱ)X表示前4局中乙当裁判的次数,求X的数学期望.
(Ⅰ)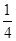 (Ⅱ)
(Ⅱ)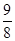
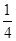 (Ⅱ)
(Ⅱ)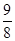
(Ⅰ)记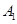 表示事件“第2局结果为甲胜”,
表示事件“第2局结果为甲胜”,
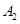 表示事件“第3局甲参加比赛时,结果为甲负”,
表示事件“第3局甲参加比赛时,结果为甲负”,
A表示事件“第4局甲当裁判”.
则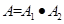 . 3分
. 3分
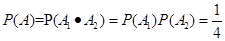 . 6分
. 6分
(Ⅱ)X的可能取值为0,1,2.
记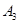 表示事件“第3局乙和丙比赛时,结果为乙胜丙”,
表示事件“第3局乙和丙比赛时,结果为乙胜丙”,
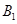 表示事件“第1局结果为乙胜丙”,
表示事件“第1局结果为乙胜丙”,
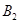 表示事件“第2局乙和甲比赛时,结果为乙胜甲”,
表示事件“第2局乙和甲比赛时,结果为乙胜甲”,
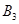 表示事件“第3局乙参加比赛时,结果为乙负”.
表示事件“第3局乙参加比赛时,结果为乙负”.
则
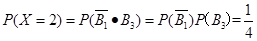 ,
,
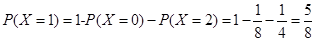 , 10分
, 10分
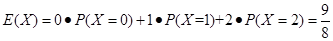 . 12分
. 12分
(1)利用独立事件的概率公式求解,关键是明确A表示事件“第4局甲当裁判”和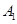 表示事件“第2局结果为甲胜”,
表示事件“第2局结果为甲胜”, 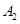 表示事件“第3局甲参加比赛时,结果为甲负”之间个独立关系;(2)明确X的可能取值,然后利用独立事件和互斥事件的公式逐一求解.因当x=1时较为复杂,故采用对立事件概率问题进行求解,即
表示事件“第3局甲参加比赛时,结果为甲负”之间个独立关系;(2)明确X的可能取值,然后利用独立事件和互斥事件的公式逐一求解.因当x=1时较为复杂,故采用对立事件概率问题进行求解,即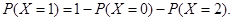
【考点定位】本题考查独立事件和互斥事件的概率问题已经离散型数学期望,考查分析问题和计算能力.
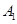 表示事件“第2局结果为甲胜”,
表示事件“第2局结果为甲胜”,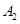 表示事件“第3局甲参加比赛时,结果为甲负”,
表示事件“第3局甲参加比赛时,结果为甲负”,A表示事件“第4局甲当裁判”.
则
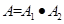 . 3分
. 3分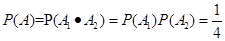 . 6分
. 6分(Ⅱ)X的可能取值为0,1,2.
记
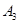 表示事件“第3局乙和丙比赛时,结果为乙胜丙”,
表示事件“第3局乙和丙比赛时,结果为乙胜丙”,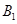 表示事件“第1局结果为乙胜丙”,
表示事件“第1局结果为乙胜丙”,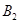 表示事件“第2局乙和甲比赛时,结果为乙胜甲”,
表示事件“第2局乙和甲比赛时,结果为乙胜甲”,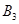 表示事件“第3局乙参加比赛时,结果为乙负”.
表示事件“第3局乙参加比赛时,结果为乙负”.则

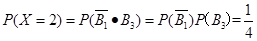 ,
,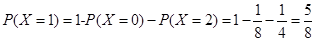 , 10分
, 10分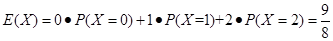 . 12分
. 12分(1)利用独立事件的概率公式求解,关键是明确A表示事件“第4局甲当裁判”和
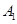 表示事件“第2局结果为甲胜”,
表示事件“第2局结果为甲胜”, 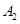 表示事件“第3局甲参加比赛时,结果为甲负”之间个独立关系;(2)明确X的可能取值,然后利用独立事件和互斥事件的公式逐一求解.因当x=1时较为复杂,故采用对立事件概率问题进行求解,即
表示事件“第3局甲参加比赛时,结果为甲负”之间个独立关系;(2)明确X的可能取值,然后利用独立事件和互斥事件的公式逐一求解.因当x=1时较为复杂,故采用对立事件概率问题进行求解,即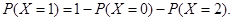
【考点定位】本题考查独立事件和互斥事件的概率问题已经离散型数学期望,考查分析问题和计算能力.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目

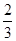 ,中将可以获得2分;方案乙的中奖率为
,中将可以获得2分;方案乙的中奖率为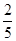 ,中将可以得3分;未中奖则不得分.每人有且只有一次抽奖机会,每次抽奖中将与否互不影响,晚会结束后凭分数兑换奖品.
,中将可以得3分;未中奖则不得分.每人有且只有一次抽奖机会,每次抽奖中将与否互不影响,晚会结束后凭分数兑换奖品.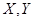 ,求
,求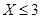 的概率;
的概率; 相切的概率;
相切的概率;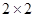 列联表;
列联表;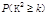
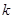
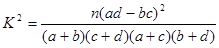 (
(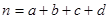 )
)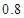 ,每个同学投篮2次,且投篮之间和同学之间都没有影响.现规定:投中两个得100分,投中一个得50分,一个未中得0分,记
,每个同学投篮2次,且投篮之间和同学之间都没有影响.现规定:投中两个得100分,投中一个得50分,一个未中得0分,记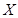 为5个同学的得分总和,则
为5个同学的得分总和,则