题目内容
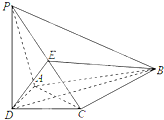
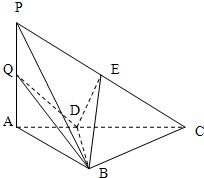
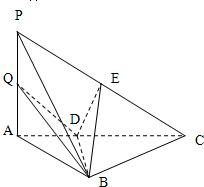
如图,三棱锥P-ABC中,PA⊥底面ABC,AB⊥BC,DE垂直平分PC,且分别交AC、PC于D、E两点,又PB=BC,PA=AB.
(Ⅰ)求证:PC⊥平面BDE;
(Ⅱ)若点Q是线段PA上任一点,求证:BD⊥DQ;
(Ⅲ)求线段PA上点Q的位置,使得PC∥平面BDQ.
(Ⅰ)求证:PC⊥平面BDE;
(Ⅱ)若点Q是线段PA上任一点,求证:BD⊥DQ;
(Ⅲ)求线段PA上点Q的位置,使得PC∥平面BDQ.

(Ⅰ)证明:由等腰三角形PBC,得BE⊥PC
又DE垂直平分PC,
∴DE⊥PC
∴PC⊥平面BDE,(4分)
(Ⅱ)由(Ⅰ),有PC⊥BD
因为PA⊥底面ABC,所以PA⊥BD
BD⊥平面PAC,所以点Q是线段PA上任一点都有
BD⊥DQ(8分)
(Ⅲ)不妨令PA=AB=1,有PB=BC=
计算得AD=
=
AC所以点Q在线段PA的
处,
即AQ=
AP时,PC∥QD,从而PC∥平面BDQ.(12分)
又DE垂直平分PC,
∴DE⊥PC
∴PC⊥平面BDE,(4分)
(Ⅱ)由(Ⅰ),有PC⊥BD
因为PA⊥底面ABC,所以PA⊥BD
BD⊥平面PAC,所以点Q是线段PA上任一点都有
BD⊥DQ(8分)
(Ⅲ)不妨令PA=AB=1,有PB=BC=
| 2 |
计算得AD=
| 3 | ||
|
| 1 |
| 3 |
| 1 |
| 3 |
即AQ=
| 1 |
| 3 |


练习册系列答案
相关题目