题目内容
【题目】已知函数f(x)=ax3-![]() x2+1(xR),其中a>0.
x2+1(xR),其中a>0.
(1)若a=1,求曲线y=f(x)在点(2,f(2))处的切线方程;
(2)若在区间![]() 上,f(x)>0恒成立,求a的取值范围.
上,f(x)>0恒成立,求a的取值范围.
【答案】(1)y=6x-9.(2)0<a<5.
【解析】试题分析:(1)利用导数求切线斜率即可;
(2)在区间![]() 上,
上,![]() 恒成立
恒成立![]() 恒成立,令
恒成立,令![]() ,解得
,解得![]() 或
或![]() ,以下分两种情况
,以下分两种情况![]() ,
,![]() 讨论,分类求出函数最大值即可.
讨论,分类求出函数最大值即可.
试题解析:(1)当a=1时,f(x)=x3-x2+1,f(2)=3;f' (x)=3x2-3x, f' (2)=6.
所以曲线y=f(x) 在点(2,f(2))处的切线方程y-3=6(x-2),即y=6x-9.
(2)f' (x)=3ax2-3x=3x(ax-1),令f' (x)=0,解得x=0或x=.
以下分两种情况讨论:
①若0<a≤2,则≥,当x变化时,f' (x),f(x)的变化情况如下表:
x | (-,0) | 0 | (0,) |
f' (x) | + | 0 | - |
f(x) | 递增 | 极大值 | 递减 |
当x[-,]上,f(x)>0等价于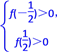 ,即
,即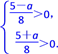 解不等式组得-5<a<5.因此0<a≤2.
解不等式组得-5<a<5.因此0<a≤2.
②若a>2,则0<<,当x变化时,f' (x),f(x)的变化情况如下表:
X | (-,0) | 0 | (0,) | (,) | |
f' (x) | + | 0 | - | 0 | + |
f'(x) | 递增 | 极大值 | 递减 | 极小值 | 递增 |
当x[-,]上,f(x)>0等价于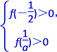 ,即
,即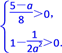 解不等式组得
解不等式组得![]() <a<5,或a<-
<a<5,或a<-![]() .因此2<a<5. 综合①和②,可知a的取值范围为0<a<5.
.因此2<a<5. 综合①和②,可知a的取值范围为0<a<5.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目