Question

【题目】已知 ．

（1）若函数的值域为，求实数的取值范围；

（2）若函数在区间上是减函数，求实数的取值范围．

Answer 1

【答案】（1） 或；（2）.

【解析】试题分析：（1）函数的值域为，即是不等式的解集为，利用二次函数性质可得判别式小于零即可得结果；（2）根据区间即是函数定义域的子集又是二次函数减区间的子集，列不等式组求解即可.

试题解析：（1）f（x）值域为R，令g（x）=x2﹣mx﹣m， 则g（x）取遍所有的正数

即△=m2+4m≥0

∴m≥0或m≤﹣4；

（2）由题意知 .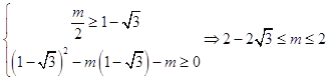

【方法点晴】本题主要考查函数的定义域、值域及利用单调性求参数的范围，属于中档题. 利用单调性求参数的范围的常见方法：① 视参数为已知数，依据函数的图象或单调性定义，确定函数的单调区间，与已知单调区间比较求参数需注意若函数在区间上是单调的，则该函数在此区间的任意子集上也是单调的; ② 利用导数转化为不等式或恒成立问题求参数范围，本题（2）是利用方法 ① 求解的．