题目内容
【题目】一儿童游乐场拟建造一个“蛋筒”型游乐设施,其轴截面如图中实线所示.ABCD是等腰梯形,AB=20米,∠CBF=α(F在AB的延长线上,α为锐角).圆E与AD,BC都相切,且其半径长为100﹣80sinα米.EO是垂直于AB的一个立柱,则当sinα的值设计为多少时,立柱EO最矮? 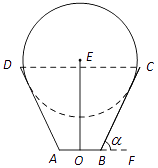
【答案】解:如图所示,以AB所在直线为x轴,以线段AB的垂直平分线为y轴,建立平面直角坐标系. 
因为B(10,0),kBC=tanα,所以直线BC的方程为:y=tanα(x﹣10),即xtanα﹣y﹣10tanα=0.
设圆心E(0,t),(t>0),由圆E与直线BC相切,得100﹣80sinα= ![]() =
= 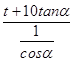 ,
,
所以EO=t= ![]() ,
,
令f(α)= ![]() ,α∈(0,
,α∈(0, ![]() ),则f′(α)=
),则f′(α)=  ,
,
设sinα0= ![]() ,α0∈(0,
,α0∈(0, ![]() ).列表如下:
).列表如下:
α | (0,α0) | α0 | (α0 , |
f′(α) | ﹣ | 0 | + |
f(α) | 减 | 极小值 | 增 |
所以当α=α0 , 即sin ![]() 时,f(α)取最小值.
时,f(α)取最小值.
答:当sin ![]() 时,立柱EO最矮.
时,立柱EO最矮.
【解析】以AB所在直线为x轴,以线段AB的垂直平分线为y轴,建立平面直角坐标系,由已知可求直线BC的方程为:xtanα﹣y﹣10tanα=0,设圆心E(0,t),(t>0),由圆E与直线BC相切,可求EO=t= ![]() ,令f(α)=
,令f(α)= ![]() ,α∈(0,
,α∈(0, ![]() ),则f′(α)=
),则f′(α)= ![]() ,设sinα0=
,设sinα0= ![]() ,α0∈(0,
,α0∈(0, ![]() ).列表可求EO的最小值.
).列表可求EO的最小值.
【考点精析】解答此题的关键在于理解正弦定理的定义的相关知识,掌握正弦定理:![]() .
.

 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案【题目】2018年俄罗斯世界杯激战正酣,某校工会对全校教职工在世界杯期间每天收看比赛的时间作了一次调查,得到如下频数分布表:
收看时间 (单位:小时) |
|
|
|
|
|
|
| 14 |
|
| 28 | 20 | 12 |
(1)若将每天收看比赛转播时间不低于3小时的教职工定义为“球迷”,否则定义为“非球迷”,请根据频数分布表补全![]() 列联表:
列联表:
男 | 女 | 合计 | |
球迷 | 40 | ||
非球迷 |
| ||
合计 |
并判断能否有90%的把握认为该校教职工是否为“球迷”与“性别”有关;
(2)在全校“球迷”中按性别分层抽样抽取6名,再从这6名“球迷”中选取2名世界杯知识讲座.记其中女职工的人数为![]() ,求的
,求的![]() 分布列与数学期望.
分布列与数学期望.
附表及公式:
| 0.15 | 0.10 | 0.05 | 0.025 |
| 2.072 | 2.706 | 3.841 | 5.024 |
![]() .
.