[题目]下面有5个命题:①函数的最小正周期是,②终边在轴上的角的集合是,③在同一坐标系中.函数的图象和函数的图象有3个公共点,④把函数的图象向右平移得到的图象,⑤角为第一象限角的充要条件是．其中.真命题的编号是．题目和参考答案——青夏教育精英家教网—

题目内容

【题目】下面有5个命题：

①函数的最小正周期是；

②终边在轴上的角的集合是；

③在同一坐标系中，函数的图象和函数的图象有3个公共点；

④把函数的图象向右平移得到的图象；

⑤角为第一象限角的充要条件是．

其中，真命题的编号是______（写出所有真命题的编号）．

【答案】①④

【解析】

利用同角三角函数的关系以及二倍角公式可判断①；利用终边相同角的写法即可判断②；研究单调性，且只有，由零点存在性定理可判断③；利用三角函数的图像变换可判断④；根据充分必要条件可判断⑤；

①函数，最小正周期是；

②终边在轴上的角的集合应该是；

③因为函数的导数，所以函数单调递增．

又易知，所以在同一坐标系中，

函数的图象和函数的图象只有一个公共点，是原点；

④把函数的图象向右平移得到，

即得到的图象；

⑤“角为第一象限角”是“”的充分不必要条件．

故答案为：①④

练习册系列答案

（1）已知小李2018年9月份上交的税费是295元，10月份月工资、薪金等税前收入与9月份相同，请帮小李计算一下税率调整后小李10月份的税后实际收入是多少？

（2）某税务部门在小李所在公司利用分层抽样方法抽取某月100位不同层次员工的税前收入，并制成下面的频率分布直方图.

（ⅰ）请根据频率分布直方图估计该公司员工税前收入的中位数；

（ⅱ）同一组中的数据以这组数据所在区间中点的值作代表，按调整后税率表，试估计小李所在的公司员工该月平均纳税多少元？

【题目】对于数列，称（其中）为数列的前k项“波动均值”.若对任意的，都有，则称数列为“趋稳数列”．

（1）若数列1，，2为“趋稳数列”，求的取值范围；

（2）若各项均为正数的等比数列的公比，求证：是“趋稳数列”；

（3）已知数列的首项为1，各项均为整数，前项的和为. 且对任意，都有，试计算：（）．

【题目】设数列满足，其中A，B是两个确定的实数，

（1）若，求的前n项和；

（2）证明：不是等比数列；

（3）若，数列中除去开始的两项外，是否还有相等的两项，并证明你的结论.

【题目】已知数列的前项和为，满足，且．正项数列满足，其前7项和为42．

（1）求数列和的通项公式；

（2）令，数列的前项和为，若对任意正整数，都有，求实数的取值范围；

（3）将数列，的项按照“当为奇数时，放在前面；当为偶数时，放在前面”的要求进行排列，得到一个新的数列：，，，，，，，，，，，…，求这个新数列的前项和．

【题目】如图,在平行四边形ABCD中,,四边形ACEF为正方形,且平面平面ACEF.

(1)证明:;

(2)求平面BEF与平面BCF所成锐二面角的余弦值.

【题目】如图，已知为等边三角形，为等腰直角三角形，.平面平面ABD，点E与点D在平面ABC的同侧，且，.点F为AD中点，连接EF.

（1）求证：平面ABC；

（2）求证：平面平面ABD.

【题目】在斜三棱柱中，，侧面是边长为4的菱形，，，、分别为、的中点.

（1）求证：平面；

（2）若，求二面角的正弦值.

【题目】国家大力提倡科技创新，某工厂为提升甲产品的市场竞争力，对生产技术进行创新改造，使甲产品的生产节能降耗．以下表格提供了节能降耗后甲产品的生产产量(吨)与相应的生产能耗(吨)的几组对照数据．

（吨）
（吨）

（1）请根据上表提供的数据，用最小二乘法求出关于的线性回归方程；

（，）

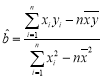（2）已知该厂技术改造前生产吨甲产品的生产能耗为吨，试根据（1）求出的线性回归方程，预测节能降耗后生产吨甲产品的生产能耗比技术改造前降低多少吨？

试题分类