题目内容
10. 在直三棱柱A1B1C1-ABC中,AC⊥BC,D、E分别为AB、AC中点.
在直三棱柱A1B1C1-ABC中,AC⊥BC,D、E分别为AB、AC中点.(1)求证:DE∥面BCC1B1;
(2)若CB=1,$AC=\sqrt{3}$,$A{A_{\;\;1}}=\sqrt{3}$.求异面直线A1E和CD所成角的大小.
分析 (1)由三角形中位线定理得DE∥BC,由此能证明DE∥面BCC1B1.
(2)取AD的中点F,连EF,A1F,则EF∥CD,∠A1EF为异面直线A1E和CD所成角(或其补角),由此能求出∠A1EF为异面直线A1E和CD所成角.
解答 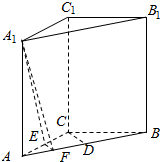 (1)证明:∵D、E分别为AB、AC中点,
(1)证明:∵D、E分别为AB、AC中点,
∴DE∥BC,…(1分)
∵BC⊆面BCC1B1…(3分)DE?面BCC1B1…(5分)
∴DE∥面BCC1B1…(6分)
(2)解:取AD的中点F,连EF,A1F,
∵EF∥CD,∴∠A1EF为异面直线A1E和CD所成角(或其补角)…(8分)
在△A1EF中,${A_1}E=\frac{{\sqrt{15}}}{2}$,$EF=\frac{1}{2}$,${A_1}F=\frac{{\sqrt{13}}}{2}$,
∴$cos∠{A_1}EF=\frac{{\sqrt{15}}}{10}$…(10分)
∴∠A1EF为异面直线A1E和CD所成角为$arccos\frac{{\sqrt{15}}}{10}$…(12分)
点评 本题考查线面平行的证明,考查异面直线所成角的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
1.函数f(x)是定义在(-2,2)上的减函数,则不等式f(x)>f(2-x)的解集为( )
| A. | (0,1) | B. | (0,2) | C. | (2,+∞) | D. | (-∞,2) |
15.已知底面是菱形的直棱柱,底面的对角线的长分别为6和8,棱柱的高为15,则这个棱柱的侧面积为( )
| A. | 75 | B. | 250 | C. | 150 | D. | 300 |
20.已知集合A={x|x2-4x-5<0,x∈N},B={y|y=ln(e-x2)},则A∩B=( )
| A. | (-1,1] | B. | {0,1} | C. | (-1,$\sqrt{e}$] | D. | {0,1,2} |
 某校从参加高一年级期中考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六段[40,50),[50,60)…[90,100]后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
某校从参加高一年级期中考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六段[40,50),[50,60)…[90,100]后得到如下部分频率分布直方图.观察图形的信息,回答下列问题: