题目内容
20.a、b、c是两两不等的实数,则经过P(b,b+c)、C(a,c+a)两点的直线的倾斜角为$\frac{π}{4}$.分析 由直线经过P(b,b+c)、C(a,c+a)两点,能求出直线AB的斜率,从而能求出直线AB的倾斜角.
解答 解:∵直线经过P(b,b+c)、C(a,c+a)两点,
∴直线AB的斜率k=$\frac{c+a-(b+c)}{a-b}$=1,
∴直线AB的倾斜角α=$\frac{π}{4}$;
故答案为:$\frac{π}{4}$.
点评 本题考查直线的倾斜角的求法,是基础题.解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
相关题目
5.已知函数f(x)=$\left\{{\begin{array}{l}{(1-3a)x+10a,x≤7}\\{{a^{x-7}},x>7}\end{array}}$是定义域(-∞,+∞)上的单调递减函数,则实数a的取值范围是( )
| A. | $(\frac{1}{3},\frac{1}{2})$ | B. | ($\frac{1}{3}$,$\frac{6}{11}$] | C. | $[\frac{1}{2},\frac{2}{3})$ | D. | $(\frac{1}{2},\frac{6}{11}]$ |
9.下列四组函数中,表示同一函数的是( )
| A. | $f(x)=|x|,g(x)=\sqrt{x^2}$ | B. | f(x)=lgx2,g(x)=2lgx | ||
| C. | $f(x)=\frac{{{x^2}-1}}{x-1},g(x)=x-1$ | D. | $f(x)=\sqrt{x+1}•\sqrt{x-1},g(x)=\sqrt{{x^2}-1}$ |
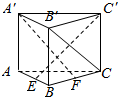 如图直三棱柱ABC-A′B′C′的侧棱长为3,AB⊥BC,且AB=BC=3,点E,F分别是棱AB,BC上的动点,且AE=BF.
如图直三棱柱ABC-A′B′C′的侧棱长为3,AB⊥BC,且AB=BC=3,点E,F分别是棱AB,BC上的动点,且AE=BF. 在直三棱柱A1B1C1-ABC中,AC⊥BC,D、E分别为AB、AC中点.
在直三棱柱A1B1C1-ABC中,AC⊥BC,D、E分别为AB、AC中点.