题目内容
18．
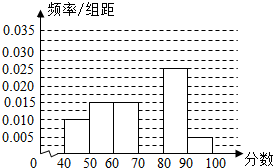某校从参加高一年级期中考试的学生中随机抽取60名学生，将其数学成绩（均为整数）分成六段[40，50），[50，60）…[90，100]后得到如下部分频率分布直方图．观察图形的信息，回答下列问题：（1）求分数在[70，80）内的频率，并补全这个频率分布直方图；
（2）求在这60名学生中分数在[60，90）的人数．
分析 （1）根据频率和为1，求出分数在[70，80）内的频率以及$\frac{频率}{组距}$，补全频率分布直方图；
（2）求出分数在[60，90）的频率与频数即可．
解答 解：（1）根据频率和为1，得；
分数在[70，80）内的频率为
1-（0.010+0.015+0.015+0.025+0.005）×10=0.3，
在频率分布直方图中，分数在[70，80）内的数据对应的矩形高为
$\frac{0.3}{10}$=0.030，
补全这个频率分布直方图，如图所示；
（2）这60名学生中分数在[60，90）的频率为
（0.015+0.030+0.025）×10=0.7，
所求的人数为60×0.7=42．
点评 本题考查了频率分布直方图的应用问题，也考查了频率=$\frac{频数}{样本容量}$的应用问题，是基础题目．
练习册系列答案
口算心算速算应用题系列答案
同步拓展阅读系列答案
相关题目
9．下列四组函数中，表示同一函数的是（ ）
| A． | $f（x）=|x|，g（x）=\sqrt{x^2}$ | B． | f（x）=lgx2，g（x）=2lgx | ||
| C． | $f（x）=\frac{{{x^2}-1}}{x-1}，g（x）=x-1$ | D． | $f（x）=\sqrt{x+1}•\sqrt{x-1}，g（x）=\sqrt{{x^2}-1}$ |
3．已知x，y满足不等式组$\left\{\begin{array}{l}{x+2y-3≤0}\\{x+3y-3≥0}\\{y≤1}\end{array}\right.$若当且仅当$\left\{\begin{array}{l}{x=3}\\{y=0}\end{array}\right.$时，z=ax+y（a＞0）取得最大值，则a的取值范围是（ ）
| A． | （0，$\frac{1}{3}$） | B． | （$\frac{1}{3}$，+∞） | C． | （0，$\frac{1}{2}$） | D． | （$\frac{1}{2}$，+∞） |
在直三棱柱A1B1C1-ABC中，AC⊥BC，D、E分别为AB、AC中点．