题目内容
4.已知抛物线y2=2px(p>0),其焦点到准线的距离与双曲线$\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{4}$=1的焦点到渐近线的距离相等,则该抛物线方程为y2=4x.分析 双曲线$\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{4}$=1的焦点($\sqrt{13}$,0)到渐近线y=$\frac{2}{3}$x的距离为$\frac{2\sqrt{13}}{\sqrt{4+9}}$=2,进而可得p,即可求出抛物线的方程.
解答 解:双曲线$\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{4}$=1的焦点($\sqrt{13}$,0)到渐近线y=$\frac{2}{3}$x的距离为$\frac{2\sqrt{13}}{\sqrt{4+9}}$=2,
∵抛物线焦点到准线的距离与双曲线$\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{4}$=1的焦点到渐近线的距离相等,
∴p=2,
∴抛物线方程为y2=4x,
故答案为:y2=4x.
点评 本题考查抛物线方程,考查抛物线的定义,考查双曲线的性质,比较基础.

练习册系列答案
相关题目
17.为了比较两种复合材料制造的轴承(分别称为类型I轴承和类型II轴承)的使用寿命,检验了两种类型轴承各30个,它们的使用寿命(单位:百万圈)如下表:
类型I
(Ⅰ)根据两组数据完成下面茎叶图;
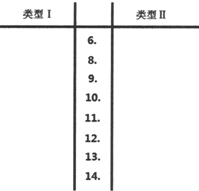
(Ⅱ)分别估计两种类型轴承使用寿命的中位数;
(Ⅲ)根据茎叶图对两种类型轴承的使用寿命进行评价.
类型I
| 6.2 | 6.4 | 8.3 | 8.6 | 9.4 | 9.8 | 10.3 | 10.6 | 11.2 | 11.4 | 11.6 | 11.6 | 11.7 | 11.8 | 11.8 |
| 1 12.2 | 12.3 | 12.3 | 12.5 | 12.5 | 12.6 | 12.7 | 12.8 | 13.3 | 13.3 | 13.4 | 13.6 | 13.8 | 14.2 | 14.5 |
| 类型II | ||||||||||||||
| 1 8.4 | 8.5 | 8.7 | 9.2 | 9.2 | 9.5 | 9.7 | 9.7 | 9.8 | 9.8 | 10.1 | 10.2 | IO.3 | 10.3 | 10.4 |
| 1 10.6 | 10.8 | 10.9 | 11.2 | 11.2 | 11.3 | 11.5 | 11.5 | 11.6 | 11.8 | 12.3 | 12.4 | 12.7 | 13.1 | 13.4 |

(Ⅱ)分别估计两种类型轴承使用寿命的中位数;
(Ⅲ)根据茎叶图对两种类型轴承的使用寿命进行评价.
16.设函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)与直线y=3的交点的横坐标构成以π为公差的等差数列,且x=$\frac{π}{6}$是f(x)的一条对称轴,则下列区间中不是函数f(x)的单调递增区间的是( )
| A. | [-$\frac{π}{3}$,0] | B. | [-$\frac{4π}{3}$,-$\frac{5π}{6}$] | C. | [$\frac{2π}{3}$,$\frac{7π}{6}$] | D. | [-$\frac{5π}{6}$,-$\frac{π}{3}$] |