题目内容
已知四棱锥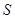 —
—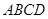 的底面
的底面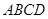 是正方形,
是正方形,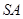 ⊥底面
⊥底面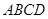 ,
,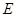 是
是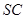 上的任意一点。
上的任意一点。
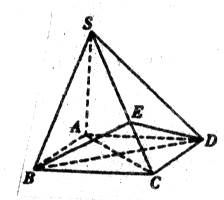
(1)求证:平面
(2)设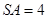 ,
,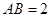 ,求点
,求点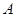 到平面的
到平面的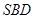 距离
距离
(3)求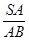 的值为多少时,二面角
的值为多少时,二面角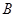 —
—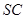 —
—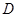 的大小为120°
的大小为120°
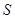 —
—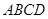 的底面
的底面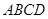 是正方形,
是正方形,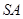 ⊥底面
⊥底面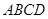 ,
,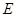 是
是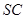 上的任意一点。
上的任意一点。
(1)求证:平面

(2)设
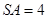 ,
,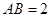 ,求点
,求点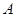 到平面的
到平面的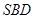 距离
距离(3)求
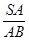 的值为多少时,二面角
的值为多少时,二面角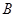 —
—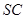 —
—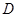 的大小为120°
的大小为120°(1)略 (2)点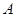 到平面
到平面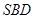 的距离为
的距离为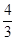
(3)当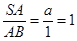 时,二面角
时,二面角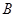 —
—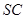 —D的大小为120°
—D的大小为120°
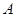 到平面
到平面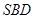 的距离为
的距离为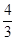
(3)当
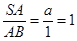 时,二面角
时,二面角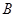 —
—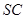 —D的大小为120°
—D的大小为120°本题考查平面与平面垂直的判定,点、线、面间的距离计算,考查逻辑思维能力,转化思想,是中档题.
(1)证明平面EBD内的直线BD,垂直平面SAC内的两条相交直线AC,SA,即可证明平面EBD⊥平面SAC;
(2)SA=4,AB=2,设AC∩BD=F,连SF,点A到平面SBD的距离为h,利用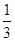 •S△SBD•h=
•S△SBD•h= 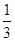 •S△ABD•SA,求点A到平面SBD的距离;
•S△ABD•SA,求点A到平面SBD的距离;
(3)利用建立空间直角坐标系,然后表示平面的法向量来求解二面角的平面角的大小
(1)证明平面EBD内的直线BD,垂直平面SAC内的两条相交直线AC,SA,即可证明平面EBD⊥平面SAC;
(2)SA=4,AB=2,设AC∩BD=F,连SF,点A到平面SBD的距离为h,利用
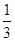 •S△SBD•h=
•S△SBD•h= 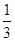 •S△ABD•SA,求点A到平面SBD的距离;
•S△ABD•SA,求点A到平面SBD的距离;(3)利用建立空间直角坐标系,然后表示平面的法向量来求解二面角的平面角的大小

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
 中,
中, 为正三角形,
为正三角形, ,
, ,
, 与
与 交于
交于 点.将
点.将 沿边
沿边 点至
点至 点,已知
点,已知 与平面
与平面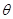 ,且
,且
 平面
平面 ;
; 的余弦值为
的余弦值为 ,求
,求 的大小.
的大小. 
 与平面
与平面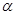 ,在平面
,在平面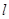 ,使
,使
 作与直线
作与直线 成
成 角的直线共有( )条
角的直线共有( )条  AB1,BN=
AB1,BN=