题目内容
【题目】如图,在三棱柱ABC﹣A1B1C1中,E,F分别为A1C1和BC的中点,M,N分别为A1B和A1C的中点.求证:
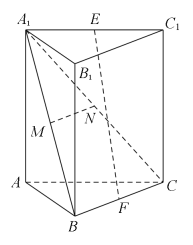
(1)MN∥平面ABC;
(2)EF∥平面AA1B1B.
【答案】(1)证明见解析;(2)证明见解析;
【解析】
(1)推导出MN∥BC,由此能证明MN∥平面ABC.
(2)取A1B1的中点D,连接DE,BD.推导出四边形DEFB是平行四边形,从而EF∥BD,由此能证明EF∥平面AA1B1B.
证明:(1)∵M、N分别是A1B和A1C中点.
∴MN∥BC,
又BC平面ABC,MN平面ABC,
∴MN∥平面ABC.
(2)如图,取A1B1的中点D,连接DE,BD.

∵D为A1B1中点,E为A1C1中点,
∴DE∥B1C1且![]() ,
,
在三棱柱ABC﹣A1B1C1中,侧面BCC1B1是平行四边形,
∴BC∥B1C1且BC=B1C1,∵F是BC的中点,∴BF∥B1C1且![]() ,
,
∴DE∥BF且DE=BF,∴四边形DEFB是平行四边形,∴EF∥BD,
又BD平面AA1B1B,EF平面AA1B1B,
∴EF∥平面AA1B1B.

练习册系列答案
相关题目