题目内容
请先阅读:
在等式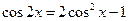 (
(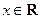 )的两边求导,得:
)的两边求导,得: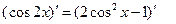 ,
,
由求导法则,得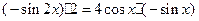 ,化简得等式:
,化简得等式: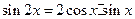 。
。
(1)利用上题的想法(或其他方法),结合等式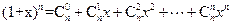 (
(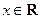 ,正整数
,正整数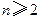 ),证明:
),证明: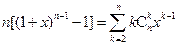 。
。
(2)对于正整数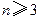 ,求证:
,求证:
(i)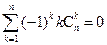 ; (ii)
; (ii)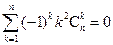 ; (iii)
; (iii)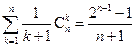 。
。
在等式
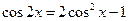 (
(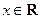 )的两边求导,得:
)的两边求导,得: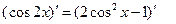 ,
,由求导法则,得
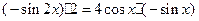 ,化简得等式:
,化简得等式: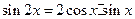 。
。(1)利用上题的想法(或其他方法),结合等式
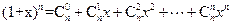 (
(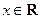 ,正整数
,正整数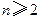 ),证明:
),证明: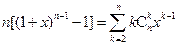 。
。(2)对于正整数
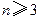 ,求证:
,求证:(i)
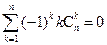 ; (ii)
; (ii)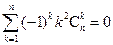 ; (iii)
; (iii)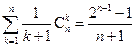 。
。(1)证明见解析。
(2)证明见解析。
(2)证明见解析。
证明:(1)在等式
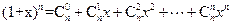 两边对
两边对 求导得
求导得
移项得
 (*)
(*)(2)(i)在(*)式中,令
 ,整理得
,整理得 
所以

(ii)由(1)知

两边对
 求导,得
求导,得
在上式中,令


即
 ,
,亦即
 (1)
(1) 又由(i)知
 (2)
(2)由(1)+(2)得
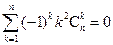
(iii)将等式
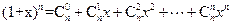 两边在
两边在 上对
上对 积分
积分
由微积分基本定理,得

所以


练习册系列答案
 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
 .
. ;
; 为
为 的一个极值点,证明
的一个极值点,证明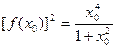 .
.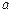 与
与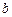 不共面,直线
不共面,直线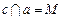 ,直线
,直线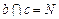 ,又
,又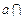 平面
平面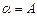 ,
,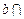 平面
平面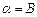 ,
,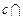 平面
平面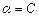 ,求证:
,求证: 三点不共线.
三点不共线.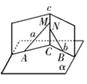
 中,若
中,若 ,则
,则 ,用类比的方法,猜想三棱锥的类似性质,并证明你的猜想
,用类比的方法,猜想三棱锥的类似性质,并证明你的猜想 ,求证:
,求证: ,用反证法证明时,可假设
,用反证法证明时,可假设 ;
; ,
, ,求证:方程
,求证:方程 的两根的绝对值都小于1.用反证法证明时可假设方程有一根
的两根的绝对值都小于1.用反证法证明时可假设方程有一根 的绝对值大于或等于1,即假设
的绝对值大于或等于1,即假设 ,以下结论正确的是( )
,以下结论正确的是( ) 与
与 的假设都错误
的假设都错误 …
… >
> (n∈N*,且n>2)时,第二步由
(n∈N*,且n>2)时,第二步由
 +
+ -
- 
 +
+
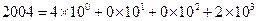 ,那么在5进制中数码2004折合成十进制为
,那么在5进制中数码2004折合成十进制为  没有最小数”时,可用反证法证明.
没有最小数”时,可用反证法证明. 是
是 中的最小数,则取
中的最小数,则取 ,可得:
,可得: ,与假设中“
,与假设中“ 是
是 没有最大数”,也可以用反证法证明.我们可以假设
没有最大数”,也可以用反证法证明.我们可以假设 是
是 中的最大数,则可以找到
中的最大数,则可以找到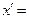 ▲ (用
▲ (用 ,
, 表示),由此可知
表示),由此可知 ,
, ,这与假设矛盾!所以数集
,这与假设矛盾!所以数集