题目内容
(1)已知函数 为有理数且
为有理数且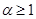 ),求函数
),求函数 的最小值;
的最小值;
(2)①试用(1)的结果证明命题 :设
:设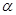 为有理数且
为有理数且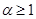 ,若
,若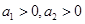 时,则
时,则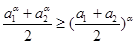 ;
;
②请将命题 推广到一般形式
推广到一般形式 ,并证明你的结论;
,并证明你的结论;
注:当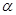 为正有理数时,有求导公式
为正有理数时,有求导公式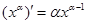
 为有理数且
为有理数且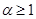 ),求函数
),求函数 的最小值;
的最小值;(2)①试用(1)的结果证明命题
 :设
:设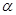 为有理数且
为有理数且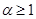 ,若
,若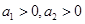 时,则
时,则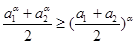 ;
;②请将命题
 推广到一般形式
推广到一般形式 ,并证明你的结论;
,并证明你的结论;注:当
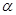 为正有理数时,有求导公式
为正有理数时,有求导公式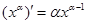
(1)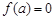 (2)①关键是利用函数的最小值为
(2)①关键是利用函数的最小值为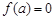 ②利用数学归纳法可证。
②利用数学归纳法可证。
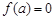 (2)①关键是利用函数的最小值为
(2)①关键是利用函数的最小值为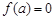 ②利用数学归纳法可证。
②利用数学归纳法可证。试题分析:解:(Ⅰ)令

得

当
 时,
时, ,故
,故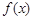 在
在 上递减.
上递减.当
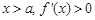 ,故
,故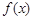 在
在 上递增.
上递增.所以,当
 时,
时,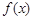 的最小值为
的最小值为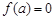
(Ⅱ)(ⅰ)
 ,令
,令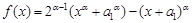 ,由(Ⅰ)知
,由(Ⅰ)知 ,
, ,即
,即
(ⅱ)命题
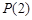 推广到一般形式
推广到一般形式 为:设
为:设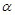 为有理数且
为有理数且 ,
,若
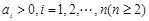 时,则
时,则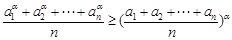 .
.下面用数学归纳法证明如下:①当
 时,由(Ⅱ)(ⅰ)知,不等式成立;
时,由(Ⅱ)(ⅰ)知,不等式成立;②假设
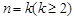 时,不等式成立,即
时,不等式成立,即 ,
,那么
 时,要证
时,要证 ,
,即证
 ,
,设函数
 ,
,则
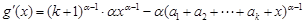 ,
,令
 ,得
,得 ,
,当
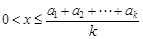 时,
时,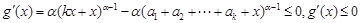 ,
,故
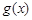 在
在 上递减;
上递减;当
 ,类似可证
,类似可证 ,故
,故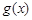 在
在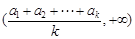 上递增.
上递增. 当
当 时,
时,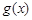 的最小值为
的最小值为

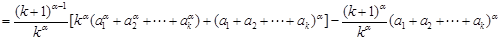

 ,
,由归纳假设知
 ,所以
,所以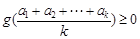 ,
,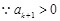 ,
,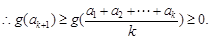
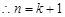 时不等式成立.
时不等式成立.综上,原命题得证
点评:本题用到的数学归纳法,在高中数学中常用来证明等式成立和数列通项公式成立。若要证明一个与自然数n有关的命题P(n),有如下步骤:
(1)证明当n取第一个值
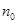 时命题成立。
时命题成立。 对于一般数列取值为0或1,但也有特殊情况;
对于一般数列取值为0或1,但也有特殊情况;(2)假设当n=k(k≥
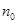 ,k为自然数)时命题成立,证明当n=k+1时命题也成立。
,k为自然数)时命题成立,证明当n=k+1时命题也成立。综合(1)(2),对一切自然数n(≥
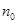 ),命题P(n)都成立。
),命题P(n)都成立。
练习册系列答案
相关题目
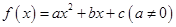 ,且不等式
,且不等式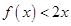 的解集为
的解集为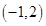 .
.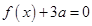 有两个相等的实根,求
有两个相等的实根,求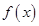 的解析式;
的解析式;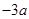 ,求实数
,求实数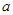 的取值范围;
的取值范围; 存在零点,并求出零点.
存在零点,并求出零点.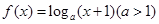 ,若函数
,若函数 图象上任意一点
图象上任意一点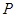 关于原点的对称点
关于原点的对称点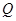 的轨迹恰好是函数
的轨迹恰好是函数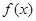 的图象.
的图象.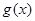 的解析式;
的解析式; 时总有
时总有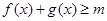 成立,求
成立,求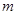 的取值范围.
的取值范围. 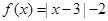 ,
,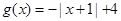 .
.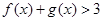 ,求
,求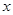 的取值范围;
的取值范围; 的解集为R,求
的解集为R,求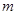 的取值范围.
的取值范围.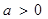 ,函数
,函数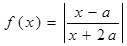 。
。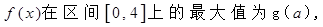 求
求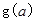 的表达式;
的表达式;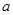 ,使函数
,使函数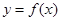 在区间
在区间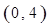 内的图像上存在两点,在该两点处的切线相互垂直?若存在,求
内的图像上存在两点,在该两点处的切线相互垂直?若存在,求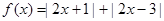 .若关于
.若关于 的不等式
的不等式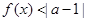 的解集非空,则实数
的解集非空,则实数 的取值范围是________.
的取值范围是________.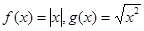
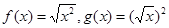

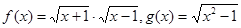
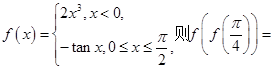 ________
________