题目内容
【题目】已知函数f(x)= 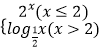 ,则函数y=f(1﹣x)的最大值为 .
,则函数y=f(1﹣x)的最大值为 .
【答案】4
【解析】解:由函数f(x)= 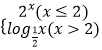 ,可得:
,可得:
x≤2时,2x≤4,且当x=2时,取得最大值4;
x>2时, ![]() x<
x< ![]() 2=﹣1.
2=﹣1.
即有函数f(x)的最大值为4;
函数f(﹣x)的图象可由f(x)的图象关于y轴对称得到,
则函数f(﹣x)的最大值为4,
函数y=f(1﹣x)的图象可由函数y=f(﹣x)图象向右平移得到.
则函数y=f(1﹣x)的最大值为4.
所以答案是:4.
【考点精析】利用函数的最值及其几何意义对题目进行判断即可得到答案,需要熟知利用二次函数的性质(配方法)求函数的最大(小)值;利用图象求函数的最大(小)值;利用函数单调性的判断函数的最大(小)值.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

