题目内容
【题目】已知数列{an}的前n项和为Sn,且满足Sn+n=2an(n∈N*).
(1)证明:数列{an+1}为等比数列,并求数列{an}的通项公式;
(2)若bn=(2n+1)an+2n+1,数列{bn}的前n项和为Tn.求满足不等式![]() >2010的n的最小值.
>2010的n的最小值.
【答案】(1)an=2n-1,n∈N*;(2)n的最小值为10.
【解析】试题分析:本题属于基础题.对已知条件![]() ,用
,用![]() 代替
代替![]() 得
得![]() ,两式相减可得
,两式相减可得![]() ,凑配得
,凑配得![]() ,由此可证得
,由此可证得![]() 是等比数列,从而求出通项公式,这是已知数列前
是等比数列,从而求出通项公式,这是已知数列前![]() 项和与项之间关系的一般处理方法;(2)由(1)可得
项和与项之间关系的一般处理方法;(2)由(1)可得![]() ,采用错位相减法可求出其前
,采用错位相减法可求出其前![]() 项和
项和![]()
![]() ,不等式>2 010就转化为
,不等式>2 010就转化为![]() ,可知n的最小值是10.
,可知n的最小值是10.
试题解析:(1)因为Sn+n=2an,所以Sn-1=2an-1-(n-1)(n≥2,n∈N*).两式相减,得an=2an-1+1.
所以an+1=2(an-1+1)(n≥2,n∈N*),所以数列{an+1}为等比数列.
因为Sn+n=2an,令n=1得a1=1.
a1+1=2,所以an+1=2n,所以an=2n-1.
(2)因为bn=(2n+1)an+2n+1,所以bn=(2n+1)·2n.
所以Tn=3×2+5×22+7×23+…+(2n-1)·2n-1+(2n+1)·2n, ①
2Tn=3×22+5×23+…+(2n-1)·2n+(2n+1)·2n+1, ②
①-②,得-Tn=3×2+2(22+23+…+2n)-(2n+1)·2n+1
=6+2×-(2n+1)·2n+1
=-2+2n+2-(2n+1)·2n+1=-2-(2n-1)·2n+1.
所以Tn=2+(2n-1)·2n+1.
若>2 010,
则>2 010,即2n+1>2 010.
由于210=1 024,211=2 048,所以n+1≥11,即n≥10.
所以满足不等式>2 010的n的最小值是10.

 寒假学与练系列答案
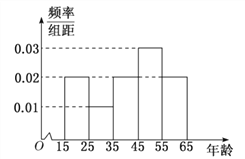
寒假学与练系列答案【题目】中央政府为了应对因人口老龄化而造成的劳动力短缺等问题,拟定出台“延迟退休年龄政策”.为了了解人们]对“延迟退休年龄政策”的态度,责成人社部进行调研.人社部从网上年龄在15![]() 65岁的人群中随机调查100人,调査数据的频率分布直方图和支持“延迟退休”的人数与年龄的统计结果如下:
65岁的人群中随机调查100人,调査数据的频率分布直方图和支持“延迟退休”的人数与年龄的统计结果如下:
年龄 |
|
|
|
|
|
支持“延迟退休”的人数 | 15 | 5 | 15 | 28 | 17 |
(1)由以上统计数据填![]() 列联表,并判断能否在犯错误的概率不超过0.05的前提下认为以45岁为分界点的不同人群对“延迟退休年龄政策”的支持度有差异;
列联表,并判断能否在犯错误的概率不超过0.05的前提下认为以45岁为分界点的不同人群对“延迟退休年龄政策”的支持度有差异;
45岁以下 | 45岁以上 | 总计 | |
支持 | |||
不支持 | /td> | ||
总计 |
(2)若以45岁为分界点,从不支持“延迟退休”的人中按分层抽样的方法抽取8人参加某项活动.现从这8人中随机抽2人
①抽到1人是45岁以下时,求抽到的另一人是45岁以上的概率.
②记抽到45岁以上的人数为![]() ,求随机变量
,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
【题目】2019年![]() 月湖北潜江将举办第六届“中国湖北(潜江)龙虾节”,为了解不同年龄的人对“中国湖北(潜江)龙虾节”关注程度,某机构随机抽取了年龄在
月湖北潜江将举办第六届“中国湖北(潜江)龙虾节”,为了解不同年龄的人对“中国湖北(潜江)龙虾节”关注程度,某机构随机抽取了年龄在![]() 岁之间的
岁之间的![]() 人进行调查,经统计“年轻人”与“中老年人”的人数之比为
人进行调查,经统计“年轻人”与“中老年人”的人数之比为![]() .
.
关注 | 不关注 | 合计 | |
年轻人 |
| ||
中老年人 | |||
合计 |
|
|
|
(1)根据已知条件完成上面的![]() 列联表,并判断能否有
列联表,并判断能否有![]() 的把握认为关注“中国湖北(潜江)龙虾节”是否和年龄段有关?
的把握认为关注“中国湖北(潜江)龙虾节”是否和年龄段有关?
(2)现已用分层抽样的办法从中老年人中选取了![]() 人进行问卷调查.若再从这
人进行问卷调查.若再从这![]() 人中选取
人中选取![]() 人进行面对面询问,求事件“选取的
人进行面对面询问,求事件“选取的![]() 人中恰有
人中恰有![]() 人关注“中国湖北(潜江)龙虾节””的概率.
人关注“中国湖北(潜江)龙虾节””的概率.
附:参考公式![]() ,其中
,其中![]() .
.
临界值表:
|
|
|
|
|
|
|
|



