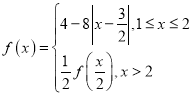题目内容
【题目】设函数f(x)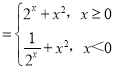 ,已知对任意的a∈[1,3],若
,已知对任意的a∈[1,3],若![]() (k∈R且k>0),恒有f(x1)≥f(x2),则k的最小值是_____.
(k∈R且k>0),恒有f(x1)≥f(x2),则k的最小值是_____.
【答案】24.
【解析】
由已知可得![]() 是偶函数,且在
是偶函数,且在![]() 为增函数,要使
为增函数,要使![]() 恒成立,只需
恒成立,只需![]() ,
,![]() ,而
,而![]() ,只需
,只需![]() ,结合
,结合![]() 范围,即可求解.
范围,即可求解.
当x>0,可得﹣x<0,f(﹣x)=2x+x2=f(x),
同样可得x<0时,f(﹣x)=f(x),且f(0)=1,
可得f(x)为偶函数,
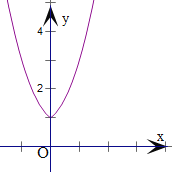
画出f(x)的图象,可得f(x)在[0,+∞)递增,
由f(x1)≥f(x2),可得f(|x1|)≥f(|x2|),即有|x1|≥|x2|,
即x12﹣x22≥0,即(x1﹣x2)(x1+x2)≥0,
由![]() (k∈R且k>0,a>0),
(k∈R且k>0,a>0),
可得x1<x2,即x1﹣x2<0,可得x1+x2≤0恒成立,
可得a![]() a
a![]() 0,即有k
0,即有k![]() ,
,
由任意的a∈[1,3],可得k![]() 24,
24,
则k的最小值为24.
故答案为:24.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某校为了了解高一新生是否愿意参加军训,随机调查了80名新生,得到如下2×2列联表
愿意 | 不愿意 | 合计 | |
男 | x | 5 | M |
女 | y | z | 40 |
合计 | N | 25 | 80 |
(1)写出表中x,y,z,M,N的值,并判断是否有99.9%的把握认为愿意参加军训与性别有关;
(2)在被调查的不愿意参加军训的学生中,随机抽出3人,记这3人中男生的人数为ξ,求ξ的分布列和数学期望.
参考公式: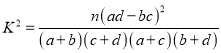
附:
P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.01 | 0.005 | 0.001 |
k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】某销售公司在当地![]() 、
、![]() 两家超市各有一个销售点,每日从同一家食品厂一次性购进一种食品,每件200元,统一零售价每件300元,两家超市之间调配食品不计费用,若进货不足食品厂以每件250元补货,若销售有剩余食品厂以每件150回收.现需决策每日购进食品数量,为此搜集并整理了
两家超市各有一个销售点,每日从同一家食品厂一次性购进一种食品,每件200元,统一零售价每件300元,两家超市之间调配食品不计费用,若进货不足食品厂以每件250元补货,若销售有剩余食品厂以每件150回收.现需决策每日购进食品数量,为此搜集并整理了![]() 、
、![]() 两家超市往年同期各50天的该食品销售记录,得到如下数据:
两家超市往年同期各50天的该食品销售记录,得到如下数据:
销售件数 | 8 | 9 | 10 | 11 |
频数 | 20 | 40 | 20 | 20 |
以这些数据的频数代替两家超市的食品销售件数的概率,记![]() 表示这两家超市每日共销售食品件数,
表示这两家超市每日共销售食品件数,![]() 表示销售公司每日共需购进食品的件数.
表示销售公司每日共需购进食品的件数.
(1)求![]() 的分布列;
的分布列;
(2)以销售食品利润的期望为决策依据,在![]() 与
与![]() 之中选其一,应选哪个?
之中选其一,应选哪个?