��Ŀ����
����Ŀ��ijУΪ���˽��һ�����Ƿ�Ը��μӾ�ѵ�����������80���������õ�����2��2������
Ը�� | ��Ը�� | �ϼ� | |
�� | x | 5 | M |
Ů | y | z | 40 |
�ϼ� | N | 25 | 80 |
��1��д������x��y��z��M��N��ֵ�����ж��Ƿ���99.9%�İ�����ΪԸ��μӾ�ѵ���Ա��йأ�
��2���ڱ�����IJ�Ը��μӾ�ѵ��ѧ���У�������3�ˣ�����3��������������Ϊ���������ķֲ��к���ѧ������
�ο���ʽ��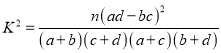
����
P��K2��k0�� | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.01 | 0.005 | 0.001 |
k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
���𰸡�(1)M��40��x��35��z��20��y��20��N��55����99.9%�İ�����ΪԸ��μ�־Ը�����ѵ���Ա��йأ�(2)�ֲ��м���⣬E(����![]() .
.
��������
��1�����ݱ��������ݣ��������x��y��z��M��N��ֵ���ټ���![]() ����ϲο����������жϣ�
����ϲο����������жϣ�
��2���г�����ȡֵ�����ݹŵ�����ʼ��㹫ʽ��÷ֲ��У��ٸ��ݷֲ��м�����ѧ��������.
��1���ɱ������ݿ�֪��
M��80��40��40��
x��40��5��35��
z��25��5��20��
y��40��20��20��
N��80��25��55��
��K2![]() 13.09��10.828��
13.09��10.828��
����99.9%�İ�����ΪԸ��μ�־Ը�����ѵ���Ա��йأ�
��2���ڱ�����IJ�Ը��μӾ�ѵ��ѧ���У�������3�ˣ�
����3��������������Ϊ���������Ŀ���ȡֵΪ0,1,2,3��
P������0��![]() ��
��
P������1��![]() ��
��
P������2��![]() ��
��
P������3��![]() ��
��
�����ķֲ���Ϊ��
�� | 0 | 1 | 2 | 3 |
P |
|
|
|
|
E������![]() ��
��

����Ŀ��ijҽ�ƴ�ѧʵϰС��Ϊ�о�ʵϰ����ҹ�²��뻼��ð����֮��Ĺ�ϵ���ֱ��������ź�ijҽԺ��¼��1�·���3�·�ÿ��5�ա�20�յ���ҹ�²��������ð��������������õ�������ϣ�
���� | 1��5�� | 1��20�� | 2��5�� | 2��20�� | 3��5�� | 3��20�� |
��ҹ�²� | 10 | 11 | 13 | 12 | 8 | 6 |
�������� | 22 | 25 | 29 | 26 | 16 | 12 |
��С��ȷ�����о������ǣ��ȴ����������������ѡȡ4�����������Իع鷽�̣�����ʣ���2�����ݽ��м���.
��1����ʣ���2��������������һ����20�յĸ��ʣ�
��2����ѡȡ����1��20�գ�2��5�գ�2��20�գ�3��5����������.
����������������ݣ����![]() ����
����![]() �����Իع鷽��
�����Իع鷽��![]() ��
��![]() ��
��![]() �÷�����ʾ����
�÷�����ʾ����
���������Իع鷽�̵õ��Ĺ���������ʣ��ļ������ݵ�����������1�ˣ�����Ϊ�õ������Իع鷽��������ģ����ʢ����������Իع鷽���Ƿ����룿
���ο���ʽ��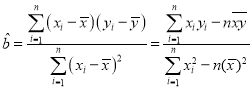 ��
��![]() .
.
����Ŀ���ĸ↑���������ҹ�ũ��7�ڶ�ƶ���˿ڰ���ƶ����ƶ����������1978���97.5%�½���2018���1.4%�������������ƶʷ�ϵ��й��漣��Ϊȫ���ƶ��ҵ�������й��ǻۺ��й���������ƶ������������ָ����ƶ���ߵ��˿�ռȫ���˿ڵı�����2012����2018���ҹ�ƶ�������ʵ��������±���
��ݣ� | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
ƶ�������� | 10.2 | 8.5 | 7.2 | 5.7 | 4.5 | 3.1 | 1.4 |
��1���ӱ���������7��ƶ����������������ѡ��������������һ������5%�ĸ��ʣ�
��2������ݴ���![]() �����ûع鷽�̣�����2012����2018��ƶ�������ʵı仯�������Ԥ��2019��ƶ�������ʣ�
�����ûع鷽�̣�����2012����2018��ƶ�������ʵı仯�������Ԥ��2019��ƶ�������ʣ�
�����ع�ֱ��![]() ��б�ʺͽؾ����С���˹��ƹ�ʽ�ֱ�Ϊ��
��б�ʺͽؾ����С���˹��ƹ�ʽ�ֱ�Ϊ��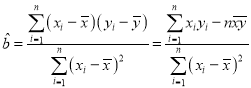 ��
��![]() ��
��