题目内容
某企业甲,乙两个研发小组,他们研发新产品成功的概率分别为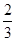 和
和 ,现安排甲组研发新产品
,现安排甲组研发新产品 ,乙组研发新产品
,乙组研发新产品 .设甲,乙两组的研发是相互独立的.
.设甲,乙两组的研发是相互独立的.
(1)求至少有一种新产品研发成功的概率;
(2)若新产品 研发成功,预计企业可获得
研发成功,预计企业可获得 万元,若新产品
万元,若新产品 研发成功,预计企业可获得利润
研发成功,预计企业可获得利润 万元,求该企业可获得利润的分布列和数学期望.
万元,求该企业可获得利润的分布列和数学期望.
(1)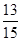 (2)详见解析
(2)详见解析
解析试题分析:(1)首先设出至少有一种新产品研发成功为事件A,包含情况较多,所以要求该事件的概率,考虑求其对立事件,即没有一种新产品研发成功,根据独立试验同时发生的概率计算方法即可求的对立事件的概率,再利用互为对立事件概率之间的关系,即和为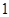 ,即可求的相应的概率.
,即可求的相应的概率.
(2)根据题意,研发新产品的结果分为四种情况,利用独立试验同时发生的概率计算方法分别得到每种情况的概率,再根据题意算出此时的利润,即可得到关于利润的分布列,再利用概率与对应的利润成绩之和即可得到数学期望.
(1)解:设至少有一组研发成功的事件为事件 且事件
且事件 为事件
为事件 的对立事件,则事件
的对立事件,则事件 为新产品
为新产品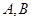 都没有成功,因为甲,乙成功的概率分别为
都没有成功,因为甲,乙成功的概率分别为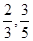 ,则
,则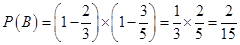 ,再根据对立事件概率之间的概率公式可得
,再根据对立事件概率之间的概率公式可得 ,所以至少一种产品研发成功的概率为
,所以至少一种产品研发成功的概率为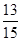 .
.
(2)由题可得设该企业可获得利润为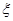 ,则
,则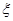 的取值有
的取值有 ,
,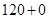 ,
,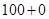 ,
,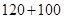 ,即
,即 ,由独立试验同时发生的概率计算公式可得:
,由独立试验同时发生的概率计算公式可得: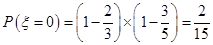 ;
;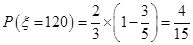 ;
;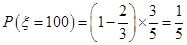 ;
;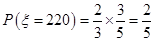 ;
;
所以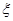 的分布列如下:
的分布列如下: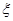



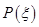
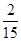
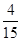
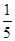
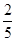
则数学期望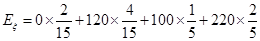
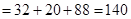 .
.
考点:分布列 数学期望 概率

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
在某学校组织的一次篮球定点投篮训练中,规定每人最多投3次:在A处每投进一球得3分,在B处每投进一球得2分;如果前两次得分之和超过3分即停止投篮,否则投第三次。某同学在A处的命中率q1为0.25,在B处的命中率为q2,该同学选择先在A处投一球,以后都在B处投,用ξ表示该同学投篮训练结束后所得的总分,其分布列为
| ξ | 0 | 2 | 3 | 4 | 5 |
| P | 0.03 | P1 | P2 | P3 | P4 |
(1)求q2的值;
(2)求随机变量ξ的数学期望E(ξ);
(3)试比较该同学选择都在B处投篮得分超过3分与选择上述方式投篮得分超过3分的概率的大小.
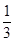 .
.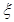 的分布列和期望.
的分布列和期望.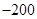 分).学科网设每次击鼓出现音乐的概率为
分).学科网设每次击鼓出现音乐的概率为 ,且各次击鼓出现音乐相互独立.
,且各次击鼓出现音乐相互独立.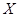 ,求
,求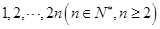 这2n个连续正整数分成A,B两组,每组n个数,A组最小数为
这2n个连续正整数分成A,B两组,每组n个数,A组最小数为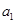 ,最大数为
,最大数为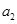 ;B组最小数为
;B组最小数为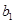 ,最大数为
,最大数为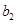 ,记
,记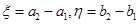
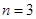 时,求
时,求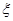 的分布列和数学期望;
的分布列和数学期望;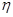 的取值恰好相等,求事件C发生的概率
的取值恰好相等,求事件C发生的概率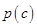 ;
;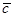 表示C的对立事件,判断
表示C的对立事件,判断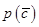 的大小关系,并说明理由。
的大小关系,并说明理由。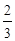 ,中奖可以获得2分;方案乙的中奖率为
,中奖可以获得2分;方案乙的中奖率为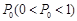 ,中奖可以获得3分;未中奖则不得分.每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,晚会结束后凭分数兑换奖品.
,中奖可以获得3分;未中奖则不得分.每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,晚会结束后凭分数兑换奖品.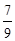 ,求
,求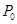 ;
;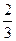 .
.