题目内容
11．已知A、B、C是球O上的三点，AB=3，BC=4，AC=5，球O到平面ABC的距离为1，求球O的表面积．分析 由题意可知三角形ACB是直角三角形，球心到平面ABC的距离为1，可求出球的半径，然后求球的表面积．
解答 解：由题意，AB=3，BC=4，AC=5，可知∠BAC=90°，
因为球心到平面ABC的距离为1，
所以球心到BC的中点的距离为1，
所以球的半径是：R=$\sqrt{1+（\frac{5}{2}）^{2}}$=$\frac{29}{4}$
球的表面积是：4πR2=29π．
点评 本题考查球的内接体问题，考查学生空间想象能力，是中档题．确定三角形ABC的形状以及利用球半径与球心O到平面ABC的距离的关系，是解好本题的前提．
练习册系列答案
百年学典课时学练测系列答案
相关题目
已知三棱柱ABC-A1B1C1中，侧棱垂直于底面，AB=5，AC=4，BC=3，AA1=4，点D在AB上．
已知一个几何体的三视图如图所示，则这个几何体的体积为$\frac{22}{3}$．
在如图所示的正方体ABCD-A1B1C1D1的12条棱所在直线中，与直线AB异面的直线有4条．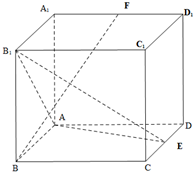
如图：在长方体ABCD-A1B1C1D1中，AB=2，BC=4，BB1=4，E是CD的中点，F是A1D1的中点．
AC=BC=$\sqrt{2}$，CD=DE=1，AB=BE=EA=2，CD⊥面ABC．