题目内容
10.如图,已知正三棱柱ABC-A1B1C1的所有棱长均为a,则异面直线BB1与A1C的距离是$\frac{\sqrt{3}}{2}a$.
分析 异面直线BB1与A1C的距离的定义,证明DE⊥AC1,ED⊥BB1,即可得到DE为AC1和BB1的公垂线.
解答  解:过B1作B1D⊥A1C1,如图
解:过B1作B1D⊥A1C1,如图
则面EFG∥面ABC∥面A1B1C1,
∴△A1B1C1为正三角形,D为A1C1的中点,B1D⊥A1C1.
又AA1⊥平面A1B1C1,∴AA1⊥B1D,
∴B1D⊥平面AA1C1C1,
∴B1D⊥A1C,
故B1D为AC1和BB1的公垂线,
∴B1D=$\frac{\sqrt{3}}{2}$a;
故答案为:$\frac{\sqrt{3}}{2}$a
点评 本题考查了异面直线的距离求法;关键是找到两条直线的公垂线,计算公垂线段的长度.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.已知空间两条直线a、b没有公共点,则a和b( )
| A. | 一定是异面直线 | B. | 一定是平行直线 | ||
| C. | 不可能是平行直线 | D. | 不可能是相交直线 |
2.在△ABC中,若tan$\frac{A}{2}$,tan$\frac{B}{2}$,tan$\frac{C}{2}$成等比数列,则角B的取值范围是( )
| A. | (0,$\frac{π}{6}$] | B. | [$\frac{π}{3}$,$\frac{2π}{3}$] | C. | (0,$\frac{π}{3}$] | D. | [$\frac{2π}{3}$,π) |
 如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E、F分别为DD1、DB的中点.
如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E、F分别为DD1、DB的中点.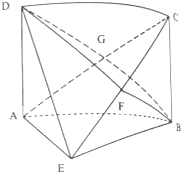 如图,在四棱锥E-ABCD中,地面ABCD为矩形,AD⊥平面ABE,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE,AC与BD相交于点G.
如图,在四棱锥E-ABCD中,地面ABCD为矩形,AD⊥平面ABE,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE,AC与BD相交于点G.