题目内容
19.某家轿车在x年的使用过程中支出,购车费12万,保险,养路,燃油费等各种费用每月共计1万元,维修费(0.1x2+0.1x)万元,使用x年后价值为(10-0.8x)万元,显然汽车年平均支出y(万元)是x的函数.(1)写出y关于x的函数关系式;
(2)探究函数的变化规律,并证明什么时候平均支出最少?
分析 (1)根据题意直接列出y关于x的函数关系式,并求出x的范围;
(2)先化简函数解析式,再利用基本不等式判断出函数的单调性,从而求出函数的最小值以及x的值.
解答 解:(1)由题意得,y=$\frac{12+12x+(0.1{x}^{2}+0.1x)-(10-0.8x)}{x}$
=$\frac{0.1{x}^{2}+12.9x+2}{x}$(x∈N+);
(2)由(1)可得,y=$0.1x+\frac{2}{x}$+12.9,
由基本不等式得,$0.1x+\frac{2}{x}≥2\sqrt{0.1x•\frac{2}{x}}$=2$\sqrt{0.2}$,
当且仅当$0.1x=\frac{2}{x}$时取等号,此时x2=20,
则函数y在(0,$\sqrt{20}$)递减,在($\sqrt{20}$,+∞)递增,
因为x取正整数,所以x取4或5,
当x=4时,y=13.8;当x=5时,y=13.8,
所以使用4或5年时平均支出最少.
点评 本题考查了函数的实际应用问题,以及基本不等式的应用,注意自变量的实际意义,属于中档题.

练习册系列答案
相关题目
 如图,四棱锥P-ABCD的底面ABCD是平行四边形,BA=BD=$\sqrt{2}$,AD=2,PA=$\sqrt{5}$,PB=$\sqrt{3}$,E,F分别是棱AD,PC的中点.
如图,四棱锥P-ABCD的底面ABCD是平行四边形,BA=BD=$\sqrt{2}$,AD=2,PA=$\sqrt{5}$,PB=$\sqrt{3}$,E,F分别是棱AD,PC的中点. 如图,AB是圆O的直径,直线CE和圆O相切于点C,AD⊥CE于D,若AD=1,∠ABC=30°,则圆O的面积是4π.
如图,AB是圆O的直径,直线CE和圆O相切于点C,AD⊥CE于D,若AD=1,∠ABC=30°,则圆O的面积是4π. 如图,在四棱锥P-ABCD中,平面PAB⊥平面ABCD,BC∥AD且2BC=AD,∠PBC=90°,∠PBA≠90°.
如图,在四棱锥P-ABCD中,平面PAB⊥平面ABCD,BC∥AD且2BC=AD,∠PBC=90°,∠PBA≠90°.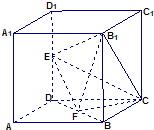 如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E、F分别为DD1、DB的中点.
如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E、F分别为DD1、DB的中点.