题目内容
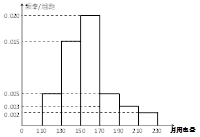
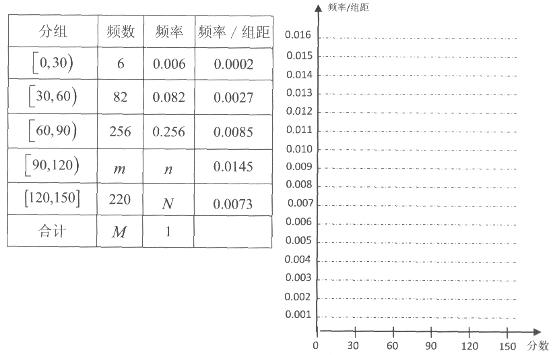
省《体育高考方案》于2012年2月份公布,方案要求以学校为单位进行体育测试,某校对高三1班同学按照高考测试项目按百分制进行了预备测试,并对50分以上的成绩进行统计,其频率分布直方图如图所示,若90~100分数段的人数为2人. 
(Ⅰ) 请估计一下这组数据的平均数M;
(Ⅱ) 现根据初赛成绩从第一组和第五组(从低分段到高分段依次为第一组、第二组、…、第五组)中任意选出两人,形成一个小组.若选出的两人成绩差大于20,则称这两人为“帮扶组”,试求选出的两人为“帮扶组”的概率.
(Ⅰ)73;(Ⅱ)选出的两人为“帮扶组”的概率为 .
.
解析试题分析:(Ⅰ)根据频率分布直方图求平均数的公式为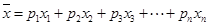 ,其中
,其中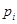 为第
为第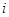 组数据的频率,
组数据的频率, 是第
是第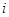 组数据的中间值.各组的频率等于小矩形的面积,由此求出各组数据的频率代入以上公式即得平均数.
组数据的中间值.各组的频率等于小矩形的面积,由此求出各组数据的频率代入以上公式即得平均数.
(Ⅱ) 90~100分数段的人数为2人,据此可求得总人数为 ,再根据频率求得50~60分数段的人数为40×0.1=4人.将第一组和第五组的同学编号,然后一一列举出所有可能结果. 两人成绩差大于20,则这两人分别来自第一组和第五组,数出其中的个数,利用古典概型概率公式便得所求概率.
,再根据频率求得50~60分数段的人数为40×0.1=4人.将第一组和第五组的同学编号,然后一一列举出所有可能结果. 两人成绩差大于20,则这两人分别来自第一组和第五组,数出其中的个数,利用古典概型概率公式便得所求概率.
试题解析:(Ⅰ) 由频率分布直方图可知:50~60分的频率为0.1,60~70分的频率为0.25,
70~80分的频率为0.45,80~90分的频率为0.15,90~100分的频率为0.05; 2分
∴这组数据的平均数M=55×0.1+65×0.25+75×0.45+85×0.15+95×0.05=73(分). 4分
(Ⅱ) ∵90~100分数段的人数为2人,频率为0.05;
∴参加测试的总人数为 =40人, 5分
=40人, 5分
∴50~60分数段的人数为40×0.1=4人, 6分
设第一组50~60分数段的同学为A1,A2,A3,A4;第五组90~100分数段的同学为B1,B2 7分
则从中选出两人的选法有:
(A1,A2),(A1,A3),(A1,A4),(A1,B1),(A1,B2),(A2,A3),(A2,A4),(A2,B1),(A2,B2),(A3,A4),(A3,B1),
(A3,B2),(A4,B1),(A4,B2),(B1,B2),共15种; 9分
其中两人成绩差大于20的选法有:(A1,B1),(A1,B2),(A2,B1),(A2,B2),
(A3,B1),(A3,B2),(A4,B1),(A4,B2)共8种 11分
则选出的两人为“帮扶组”的概率为P=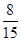 12分
12分
考点:1、频率分布直方图;2、古典概型.

某学校的三个学生社团的人数分布如下表(每名学生只能参加一个社团):
| | 围棋社 | 舞蹈社 | 拳击社 |
| 男生 | 5 | 10 | 28 |
| 女生 | 15 | 30 | m |
(Ⅰ)求拳击社女生有多少人;
(Ⅱ)从围棋社指定的3名男生和2名女生中随机选出2人参加围棋比赛,求这两名同学是一名男生和一名女生的概率.
已知某中学高三文科班学生的数学与地理的水平测试成绩抽样统计如下表:
 | A | B | C |
| A | 7 | 20 | 5 |
| B | 9 | 18 | 6 |
| C | a | 4 | b |
(1)若在该样本中,数学成绩优秀率是30%,求a,b的值;
(2)在地理成绩为C等级的学生中,已知a≥10,b≥8,求数学成绩为A等级的人数比C等级的人数少的概率.
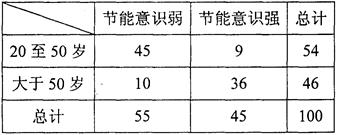
在对人们的休闲方式的一次调查中,共调查了124人,其中女性70人,男性54人。女性中有43人主要的休闲方式是看电视,另外27人主要的休闲方式是运动;男性中有21人主要的休闲方式是看电视,另外33人主要的休闲方式是运动。
(Ⅰ)根据以上数据建立一个2×2列联表;
(Ⅱ)试判断是否有97.5%的把握认为“休闲方式与性别有关”?
下面临界值表仅供参考:
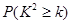 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
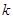 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
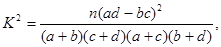 其中
其中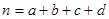 )
) 
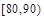 、
、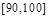 上的概率.
上的概率.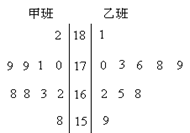
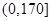 ,第二类在
,第二类在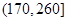 ,第三类在
,第三类在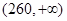 (单位:千瓦时). 某小区共有1000户居民,现对他们的用电情况进行调查,得到频率分布直方图如图所示.
(单位:千瓦时). 某小区共有1000户居民,现对他们的用电情况进行调查,得到频率分布直方图如图所示.