题目内容
在对人们的休闲方式的一次调查中,共调查了124人,其中女性70人,男性54人。女性中有43人主要的休闲方式是看电视,另外27人主要的休闲方式是运动;男性中有21人主要的休闲方式是看电视,另外33人主要的休闲方式是运动。
(Ⅰ)根据以上数据建立一个2×2列联表;
(Ⅱ)试判断是否有97.5%的把握认为“休闲方式与性别有关”?
下面临界值表仅供参考:
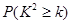 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
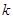 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
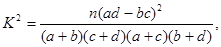 其中
其中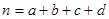 )
)
(I)2×2列联表
(II)有97.5%的把握认为“休闲方式与性别有关”性别 休闲方式 看电视 运动 总计 女 43 27 70 男 21 33 54 总计 64 60 124
解析试题分析:(I)直接根据所给数据写出2×2列联表 假设关于某设备的使用年限x和所支出的维修费用y(万元)有如下的统计资料: 为预防H7N9病毒爆发,某生物技术公司研制出一种H7N9病毒疫苗,为测试该疫苗的有效性(若疫苗有效的概率小于90%,则认为测试没有通过),公司选定2000个样本分成三组,测试结果如下表: (本小题满分12分) 第
(II)假设“休闲方式与性别无关”应用“卡方公式”加以计算得到:性别 休闲方式 看电视 运动 总计 女 43 27 70 男 21 33 54 总计 64 60 124 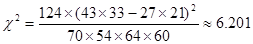 ,对比临界值表,做出判断.本题中
,对比临界值表,做出判断.本题中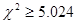 ,所以有理由认为假设“休闲方式与性别无关”是不合理的,即有97.5%的把握认为“休闲方式与性别有关”.
,所以有理由认为假设“休闲方式与性别无关”是不合理的,即有97.5%的把握认为“休闲方式与性别有关”.
试题解析:(I)2×2列联表性别 休闲方式 看电视 运动 总计 女 43 27 70 男 21 33 54 总计 64 
绩优中考系列答案
课堂追踪系列答案
活力英语课课练与单元检测系列答案
名师课时计划系列答案
全优AB卷系列答案
品优课堂系列答案
核心课堂武汉大学出版社系列答案
冠军练加考系列答案
考点集训与满分备考系列答案
课堂小测6分钟系列答案
(1)画出散点图;使用年限x 2 3 4 5 6 维修费用y 2.2 3.8 5.5 6.5 7.0
(2)若线性相关,则求出回归方程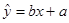 ;
;
(3)估计使用年限为10年时,维修费用是多少?
(参考公式: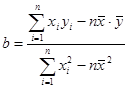 ,
, )
)
已知在全体样本中随机抽取1个,抽到B组疫苗有效的概率是0.33.分组
A组
B组
C组
疫苗有效
673
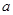
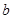
疫苗无效
77
90
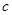
(1)现用分层抽样的方法在全体样本中抽取360个测试结果,应在C组抽取样本多少个?
(2)已知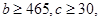 求通过测试的概率.
求通过测试的概率.
某学校高二年级共有1000名学生,其中男生650人,女生350人,为了调查学生周末的休闲方式,用分层抽样的方法抽查了200名学生.
(1)完成下面的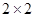 列联表;
列联表;
(2)在喜欢运动的女生中调查她们的运动时间, 发现她们的运动时间介于30分钟到90分钟之间,如图是测量结果的频率分布直方图,若从区间段
不喜欢运动
喜欢运动
合计
女生
50
男生
合计
100
200
 和
和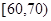 的所有女生中随机抽取两名女生,求她们的运动时间在同一区间段的概率.
的所有女生中随机抽取两名女生,求她们的运动时间在同一区间段的概率.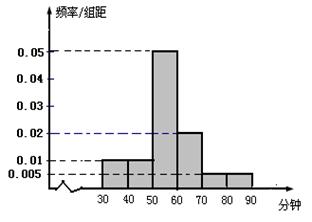
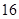 届亚运会于
届亚运会于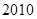 年
年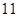 月
月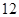 日至
日至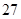 日在中国广州进行,为了做好接待工作,组委会招募了
日在中国广州进行,为了做好接待工作,组委会招募了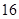 名男志愿者和
名男志愿者和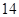 名女志愿者,调查发现,男、女志愿者中分别有
名女志愿者,调查发现,男、女志愿者中分别有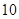 人和
人和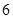 人喜爱运动,其余不喜爱.
人喜爱运动,其余不喜爱.
根据以上数据完成以下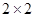 列联表:
列联表:
(2)能否在犯错误的概率不超过 喜爱运动 不喜爱运动 总计 男 10 16 女 6 14 总计 30 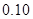 的前提下认为性别与喜爱运动有关?
的前提下认为性别与喜爱运动有关?
(3)如果从喜欢运动的女志愿者中(其中恰有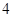 人会外语),抽取
人会外语),抽取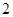 名负责翻译工作,则抽出的志愿者中
名负责翻译工作,则抽出的志愿者中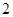 人都能胜任翻译工作的概率是多少?
人都能胜任翻译工作的概率是多少?
附:K2=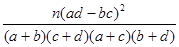
P(K2≥k) 0.100 0.050 0.025 0.010 0.001 k 2.706 3.841 5.024 6.635 10.828
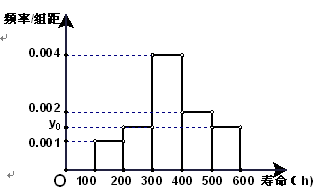
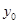 处刻度不清,根据图表所提供的数据还原
处刻度不清,根据图表所提供的数据还原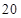 个元件,寿命为
个元件,寿命为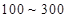 之间的应抽取几个;
之间的应抽取几个; 个元件,求事件“恰好有一个寿命为
个元件,求事件“恰好有一个寿命为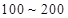 ,一个寿命为
,一个寿命为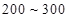 ”的概率.
”的概率.
 ,第2组
,第2组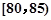 ,第3组
,第3组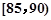 ,第4组
,第4组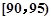 ,第5组
,第5组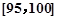 ,得到的频率分布直方图如图所示,同时规定成绩在85分以上(含85分)的学生为“优秀”,成绩小于85分的学生为“良好”,且只有成绩为“优秀”的学生才能获得面试资格.
,得到的频率分布直方图如图所示,同时规定成绩在85分以上(含85分)的学生为“优秀”,成绩小于85分的学生为“良好”,且只有成绩为“优秀”的学生才能获得面试资格. ,其中第二小组的频数为12.
,其中第二小组的频数为12.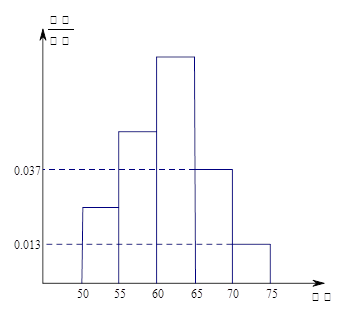
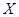 表示体重超过60公斤的学生人数,求
表示体重超过60公斤的学生人数,求