题目内容
某学校的三个学生社团的人数分布如下表(每名学生只能参加一个社团):
| | 围棋社 | 舞蹈社 | 拳击社 |
| 男生 | 5 | 10 | 28 |
| 女生 | 15 | 30 | m |
(Ⅰ)求拳击社女生有多少人;
(Ⅱ)从围棋社指定的3名男生和2名女生中随机选出2人参加围棋比赛,求这两名同学是一名男生和一名女生的概率.
(Ⅰ) ;(Ⅱ)
;(Ⅱ)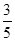 .
.
解析试题分析:(Ⅰ)根据分层抽样的要求,每层的抽样比相等,所以有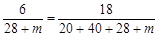 ,解此方程可得
,解此方程可得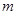 的值.(Ⅱ)从围棋社指定的3名男生和2名女生中随机选出2人,共有10种不同的方法,由于是随机抽取的,每个结果出现的可能性是相等的,故可用古典概型.
的值.(Ⅱ)从围棋社指定的3名男生和2名女生中随机选出2人,共有10种不同的方法,由于是随机抽取的,每个结果出现的可能性是相等的,故可用古典概型.
试题解析:(Ⅰ)由于按分层抽样的方法从三个社团成员中抽取18人,拳击社被抽出了6人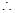
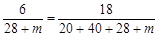
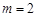 6分
6分
(Ⅱ)从围棋社指定的3名男生和2名女生中随机选出2人,共有10种不同的方法,由于是随机抽取的,每个结果出现的可能性是相等的;设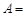 “这两名同学是一名男生和一名女生”,则事件
“这两名同学是一名男生和一名女生”,则事件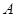 共包含6个基本事件,
共包含6个基本事件,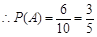 12分
12分
考点:1、分层抽样;2、古典概型.

练习册系列答案
相关题目
某城市随机抽取一年(365天)内100天的空气质量指数API的监测数据,结果统计如下:
| API | 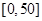 | 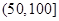 | 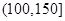 | 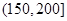 |  | 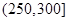 | 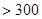 |
| 空气质量 | 优 | 良 | 轻微污染 | 轻度污染 | 中度污染 | 中重度污染 | 重度污染 |
| 天数 | 4 | 13 | 18 | 30 | 9 | 11 | 15 |
 ,试估计在本年度内随机抽取一天,该天经济损失S大于200元且不超过600元的概率;
,试估计在本年度内随机抽取一天,该天经济损失S大于200元且不超过600元的概率;(2)若本次抽取的样本数据有30天是在供暖季,其中有8天为重度污染完成下面
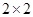 列联表,并判断能否有
列联表,并判断能否有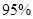 的把握认为该市本年空气重度污染与供暖有关?
的把握认为该市本年空气重度污染与供暖有关?附:
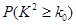 | 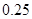 | 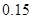 | 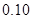 | 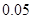 | 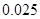 | 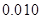 |  | 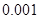 |
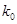 | 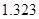 | 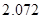 | 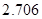 | 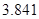 |  | 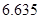 | 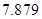 | 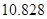 |
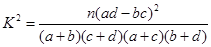
| | 非重度污染 | 重度污染 | 合计 |
| 供暖季 | | | |
| 非供暖季 | | | |
| 合计 | | | 100 |
2013年9月20日是第25个全国爱牙日。某区卫生部门成立了调查小组,调查 “常吃零食与患龋齿的关系”,对该区六年级800名学生进行检查,按患龋齿和不患龋齿分类,得汇总数据:不常吃零食且不患龋齿的学生有60名,常吃零食但不患龋齿的学生有100名,不常吃零食但患龋齿的学生有140名.
 | 0.010 | 0.005 | 0.001 |
 | 6.635 | 7.879 | 10.828 |
(1)能否在犯错概率不超过0.001的前提下,认为该区学生的常吃零食与患龋齿有关系?
(2)4名区卫生部门的工作人员随机分成两组,每组2人,一组负责数据收集,另一组负责数据处理.求工作人员甲分到负责收集数据组,工作人员乙分到负责数据处理组的概率.
附:


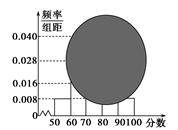
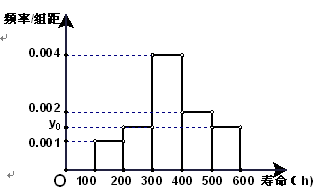
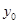 处刻度不清,根据图表所提供的数据还原
处刻度不清,根据图表所提供的数据还原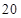 个元件,寿命为
个元件,寿命为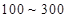 之间的应抽取几个;
之间的应抽取几个; 个元件,求事件“恰好有一个寿命为
个元件,求事件“恰好有一个寿命为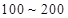 ,一个寿命为
,一个寿命为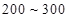 ”的概率.
”的概率.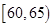 ,
, ,
, ,
, ,
, ,
, 后得到如图的频率分布直方图。问:
后得到如图的频率分布直方图。问:
 中的车辆中任取2辆,求抽出的2辆中速度在
中的车辆中任取2辆,求抽出的2辆中速度在 的分布列及其数学期望。(12分)
的分布列及其数学期望。(12分)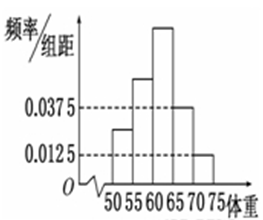

 ,其中第二小组的频数为12.
,其中第二小组的频数为12.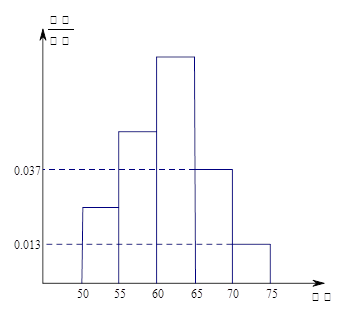
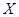 表示体重超过60公斤的学生人数,求
表示体重超过60公斤的学生人数,求