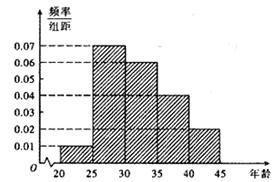
题目内容
某小区在一次对20岁以上居民节能意识的问卷调查中,随机抽取了100份问卷进行统计,得到相关的数据如下表: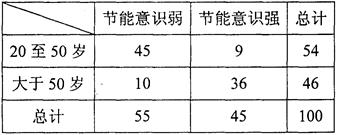
(Ⅰ)由表中数据直观分析,节能意识强弱是否与人的年龄有关?
(Ⅱ)据了解到,全小区节能意识强的人共有350人,估计这350人中,年龄大于50岁的有多少人?
(Ⅲ)按年龄分层抽样,从节能意识强的居民中抽5人,再从这5人中任取2人,求恰有1人年龄在20至50岁的概率.
(Ⅰ)节能意识强弱与年龄有关;(Ⅱ)年龄大于50岁的有280人;(Ⅲ)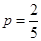 .
.
解析试题分析:(Ⅰ)因为20至50岁的54人有9人节能意识强,大于50岁的46人有36人节能意识强,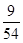 与
与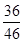 相差较大,所以节能意识强弱与年龄有关;(Ⅱ)根据比例即可求得年龄大于50岁的人数;(Ⅲ)分层抽样就是按比例抽样,根据比例可求得,年龄在20至50岁的抽1人,年龄大于50岁的抽4人,记这5人分别为A,B1,B2,B3,B4,从这5人中任取2人,将其结果一一列举出来,共有10种不同的结果,数出其中“恰有1人年龄在20至50岁”的基本事件的个数,即可得所求概率.
相差较大,所以节能意识强弱与年龄有关;(Ⅱ)根据比例即可求得年龄大于50岁的人数;(Ⅲ)分层抽样就是按比例抽样,根据比例可求得,年龄在20至50岁的抽1人,年龄大于50岁的抽4人,记这5人分别为A,B1,B2,B3,B4,从这5人中任取2人,将其结果一一列举出来,共有10种不同的结果,数出其中“恰有1人年龄在20至50岁”的基本事件的个数,即可得所求概率.
试题解析:(Ⅰ)因为20至50岁的54人有9人节能意识强,大于50岁的46人有36人节能意识强,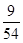 与
与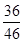 相差较大 1分,所以节能意识强弱与年龄有关 2分
相差较大 1分,所以节能意识强弱与年龄有关 2分
(Ⅱ)年龄大于50岁的有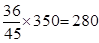 (人) 5分(列式2分,结果1分)
(人) 5分(列式2分,结果1分)
(Ⅲ)抽取节能意识强的5人中,年龄在20至50岁的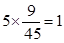 (人) 8分,
(人) 8分,
年龄大于50岁的4人 8分,记这5人分别为A,B1,B2,B3,B4。
从这5人中任取2人,共有10种不同取法 9分
完全正确列举 10分
设A表示随机事件“这5人中任取2人,恰有1人年龄在20至50岁”,则A中的基本事件有4种:完全正确列举 11分
故所求概率为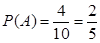 12分
12分
考点:1、统计基础知识;2、古典概型.

假设关于某设备的使用年限x和所支出的维修费用y(万元)有如下的统计资料:
| 使用年限x | 2 | 3 | 4 | 5 | 6 |
| 维修费用y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
(2)若线性相关,则求出回归方程
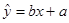 ;
;(3)估计使用年限为10年时,维修费用是多少?
(参考公式:
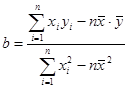 ,
, )
) (本小题满分12分)
某学校高二年级共有1000名学生,其中男生650人,女生350人,为了调查学生周末的休闲方式,用分层抽样的方法抽查了200名学生.
(1)完成下面的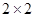 列联表;
列联表;
| | 不喜欢运动 | 喜欢运动 | 合计 |
| 女生 | 50 | | |
| 男生 | | | |
| 合计 | | 100 | 200 |
 和
和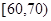 的所有女生中随机抽取两名女生,求她们的运动时间在同一区间段的概率.
的所有女生中随机抽取两名女生,求她们的运动时间在同一区间段的概率.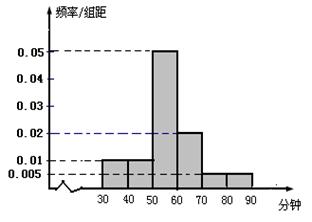
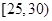 ,第2组
,第2组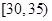 ,第3组
,第3组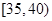 ,第4组
,第4组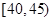 ,第5组
,第5组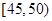 ,得到的频率分布直方图如图所示,下表是年龄的频率分布表.
,得到的频率分布直方图如图所示,下表是年龄的频率分布表.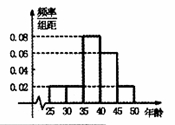

 的值;
的值;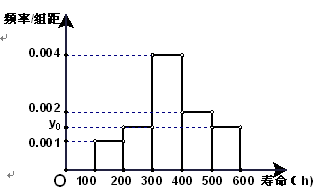
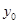 处刻度不清,根据图表所提供的数据还原
处刻度不清,根据图表所提供的数据还原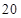 个元件,寿命为
个元件,寿命为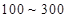 之间的应抽取几个;
之间的应抽取几个; 个元件,求事件“恰好有一个寿命为
个元件,求事件“恰好有一个寿命为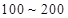 ,一个寿命为
,一个寿命为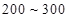 ”的概率.
”的概率.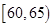 ,
, ,
, ,
, ,
, ,
, 后得到如图的频率分布直方图。问:
后得到如图的频率分布直方图。问:
 中的车辆中任取2辆,求抽出的2辆中速度在
中的车辆中任取2辆,求抽出的2辆中速度在 的分布列及其数学期望。(12分)
的分布列及其数学期望。(12分)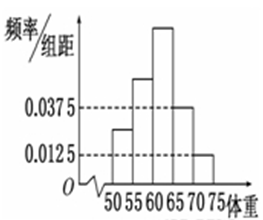
 ,第2组
,第2组 ,第3组
,第3组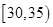 ,第4组
,第4组 ,第5组
,第5组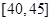 ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.