题目内容
已知数列{an}满足a1=3,a2=6,an+2=an+1-an,则a2014=( )
| A.6 | B.-3 | C.-6 | D.3 |
∵an+2=an+1-an,
∴an+3=an+2-an+1=an+1-an-an+1=-an,
即an+6=-an+3=an,
即数列{an}是周期为6的周期数列.
∴a2014=a335×6+4=a4,
∵a1=3,a2=6,an+2=an+1-an,
∴a3=a2-a1=6-3=3,a4=a3-a2=3-6=-3.
故a2014=a4=-3.
故选:B.
∴an+3=an+2-an+1=an+1-an-an+1=-an,
即an+6=-an+3=an,
即数列{an}是周期为6的周期数列.
∴a2014=a335×6+4=a4,
∵a1=3,a2=6,an+2=an+1-an,
∴a3=a2-a1=6-3=3,a4=a3-a2=3-6=-3.
故a2014=a4=-3.
故选:B.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案
相关题目
 中,
中, ,求数列
,求数列 为数列
为数列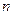 项和,
项和, ,
, ,求数列
,求数列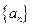 满足
满足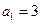 ,
,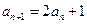 ,试写出该数列的前
,试写出该数列的前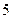 项,并用观察法写出这个数列的一个通项公式.
项,并用观察法写出这个数列的一个通项公式.
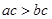 ,则
,则
 ,则
,则 ,则
,则
 ,则
,则