已知$\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$=$\overrightarrow{0}$.且|$\overrightarrow{a}$|=3.|$\overrightarrow{b}$|=1.|$\overrightarrow{c}$|=4.计算:$\overrightarrow{a}$•$\overrig 题目和参考答案——青夏教育精英家教网——

题目内容

20．已知$\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$=$\overrightarrow{0}$，且|$\overrightarrow{a}$|=3，|$\overrightarrow{b}$|=1，|$\overrightarrow{c}$|=4，计算：$\overrightarrow{a}$•$\overrightarrow{b}$+$\overrightarrow{b}$•$\overrightarrow{c}$+$\overrightarrow{c}$•$\overrightarrow{a}$．

分析可将$\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$=$\overrightarrow{0}$两边平方，结合向量的平方即为模的平方，计算即可得到所求．

解答解：由|$\overrightarrow{a}$|=3，|$\overrightarrow{b}$|=1，|$\overrightarrow{c}$|=4，
$\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$=$\overrightarrow{0}$，
平方可得，$\overrightarrow{a}$²+$\overrightarrow{b}$²+$\overrightarrow{c}$²+2（$\overrightarrow{a}$•$\overrightarrow{b}$+$\overrightarrow{b}$•$\overrightarrow{c}$+$\overrightarrow{c}$•$\overrightarrow{a}$）=0，
即有$\overrightarrow{a}$•$\overrightarrow{b}$+$\overrightarrow{b}$•$\overrightarrow{c}$+$\overrightarrow{c}$•$\overrightarrow{a}$=-$\frac{1}{2}$（$\overrightarrow{a}$²+$\overrightarrow{b}$²+$\overrightarrow{c}$²）
=-$\frac{1}{2}$（9+1+16）=-13．

点评本题考查向量的数量积的性质：向量的平方即为模的平方，考查运算能力，属于基础题．

练习册系列答案

全品作业本系列答案

全品小复习系列答案

全品基础小练习系列答案

全品学练考系列答案

实验班提优训练系列答案

启东中学作业本系列答案

综合应用创新题典中点系列答案

特高级教师点拨系列答案

名校课堂内外系列答案

课堂点睛系列答案

相关题目

11．已知函数f（x）为定义在R上的奇函数，当x＞0时，都有f（x+$\frac{3}{2}$）f（x）=2014，且当x∈（0，$\frac{3}{2}$]时，f（x）=log₂（2x+1），则f（-2015）+f（2013）=-2014．

11．为了给灾区募捐，国家发行了一种福利彩票，这种彩票的开奖规则是从1，2，…，36中任意选出7个基本号码．凡购买的彩票上的7个号码中有4个或4个以上基本号码就中奖，根据彩票上含有基本号码的个数的多少，中奖的等级为：

含有基本号码个数	4	5	6	7
中奖等级	四等奖	三等奖	二等奖	一等奖

求至少中三等奖的概率．（结果保留一位有效数字）

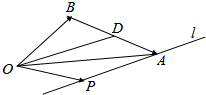在△OAB中，D是线段AB的中点，过点A的直线l∥OD，P是直线l上的动点，若$\overrightarrow{OP}$=λ₁$\overrightarrow{OA}$+λ₂$\overrightarrow{OB}$，则λ₁-λ₂=1．

15．已知曲线C的极坐标方程是ρ=2cos（θ+$\frac{π}{3}$），以极点为平面直角坐标系的原点，极轴为x轴的正半轴，且取相等的单位长度，建立平面直角坐标系，直线l的参数方程是$\left\{\begin{array}{l}{x=-1-t}\\{y=2+\sqrt{3}t}\end{array}\right.$（t是参数），设点P（-1，2）
（Ⅰ）将曲线C的极坐标方程为直角坐标方程，将直线l的参数方程化为普通方程；
（Ⅱ）设直线l与曲线C相交于M，N两点，求|PM|•|PN|的值．

5．函数f（x）=2ax²-2bx-a+b（a，b∈R，a＞0），若θ∈[0，$\frac{π}{2}$]时，求f（sinθ）的最大值．

12．在△ABC中，若$\overrightarrow{AB}$•$\overrightarrow{BC}$＞0，则角B的取值范围是（　　）

[$\frac{π}{2}$，π）

（$\frac{π}{2}$，π）

（0，$\frac{π}{2}$]

（0，$\frac{π}{2}$）

9．计算下列各式：
（1）|1+lg0.001|+$\sqrt{{lg}^{2}\frac{1}{2}-4lg2+4}$+lg6-lg0.03；
（2）（0.001）${\;}^{-\frac{1}{3}}$+（27）${\;}^{\frac{2}{3}}$-（$\frac{1}{4}$）${\;}^{-\frac{1}{2}}$+（$\frac{1}{9}$）^-1.5．

10．已知f（x）-2f（$\frac{1+x}{1-x}$）=7x，求f（x）