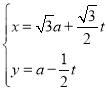题目内容
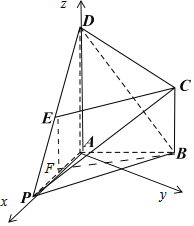
【题目】如图,在四棱锥P﹣ABCD中AD∥BC,DA⊥AB,AD=2,AB=BC=1,CD![]() ,点E为PD中点.
,点E为PD中点.
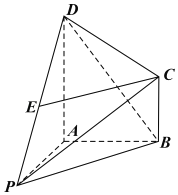
(1)求证:CE∥平面PAB;
(2)若PA=2,PD=2![]() ,∠PAB
,∠PAB![]() ,求平面PBD与平面ECD所成锐二面角的余弦值.
,求平面PBD与平面ECD所成锐二面角的余弦值.
【答案】(1)见解析;(2)![]()
【解析】
(1)取AP的中点F,连接EF,FB,证明平行四边形EFBC,得到证明.
(2)以A为原点,以AP为x轴,过A垂直于AP的直线为y轴,以AD为z轴建立空间直角坐标系,平面PBD的法向量为![]() ,平面ECD的法向量为
,平面ECD的法向量为![]() ,计算夹角得到答案.
,计算夹角得到答案.
(1)取AP的中点F,连接EF,FB,则EF∥AD,且EF![]() ,
,
由AD∥BC,且BC![]() ,故EF∥BC,且EF=BC,
,故EF∥BC,且EF=BC,
故平行四边形EFBC,由EC平面PAB,BF平面PAB,
故EC∥平面PAB;
(2)PA=2,PD=2![]() ,AD=2,所以AD⊥AP,由DA⊥AB,易知AD⊥平面PAB,
,AD=2,所以AD⊥AP,由DA⊥AB,易知AD⊥平面PAB,
以A为原点,以AP为x轴,过A垂直于AP的直线为y轴,以AD为z轴建立空间直角坐标系,
P(2,0,0),B(![]() ,0),D(0,0,2),C(
,0),D(0,0,2),C(![]() ),E(1,0,1),
),E(1,0,1),
设平面PBD的法向量为![]() ,
,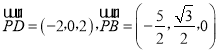 ,
,
由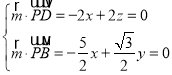 ,得
,得![]() ,
,
设平面ECD的法向量为![]() ,
,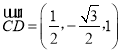 ,
,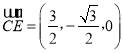 ,
,
由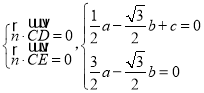 ,得
,得![]() ,
,
由cos![]() ,
,
故平面PBD与平面ECD所成锐二面角的余弦值为![]() .
.

【题目】在世界读书日期间,某地区调查组对居民阅读情况进行了调查,获得了一个容量为200的样本,其中城镇居民140人,农村居民60人.在这些居民中,经常阅读的城镇居民有100人,农村居民有30人.
(1)填写下面列联表,并判断能否有99%的把握认为经常阅读与居民居住地有关?
城镇居民 | 农村居民 | 合计 | |
经常阅读 | 100 | 30 | |
不经常阅读 | |||
合计 | 200 |
(2)从该地区城镇居民中,随机抽取5位居民参加一次阅读交流活动,记这5位居民中经常阅读的人数为![]() ,若用样本的频率作为概率,求随机变量
,若用样本的频率作为概率,求随机变量![]() 的期望.
的期望.
附: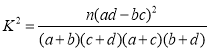 ,其中
,其中![]() .
.
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】BMI指数是用体重公斤数除以身高米数的平方得出的数值,是国际上常用的衡量人体胖瘦程度以及是否健康的一个标准.对于高中男体育特长生而言,当BMI数值大于或等于20.5时,我们说体重较重,当BMI数值小于20.5时,我们说体重较轻,身高大于或等于170cm时,我们说身高较高,身高小于170cm时,我们说身高较矮.某中小学生成长与发展机构从某市的320名高中男体育特长生中随机选取8名,其身高和体重的数据如表所示:
编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
身高(cm) | 166 | 167 | 160 | 173 | 178 | 169 | 158 | 173 |
体重(kg) | 57 | 58 | 53 | 61 | 66 | 57 | 50 | 66 |
(1)根据最小二乘法的思想与公式求得线性回归方程![]() .利用已经求得的线性回归方程,请完善下列残差表,并求解释变量(身高)对于预报变量(体重)变化的贡献值
.利用已经求得的线性回归方程,请完善下列残差表,并求解释变量(身高)对于预报变量(体重)变化的贡献值![]() (保留两位有效数字);
(保留两位有效数字);
编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
身高(cm) | 166 | 167 | 160 | 173 | 178 | 169 | 158 | 173 |
体重(kg) | 57 | 58 | 53 | 61 | 66 | 57 | 50 | 66 |
残差 | 0.1 | 0.3 | 0.9 | ﹣1.5 | ﹣0.5 |
(2)通过残差分析,对于残差的最大(绝对值)的那组数据,需要确认在样本点的采集中是否有人为的错误.已知通过重新采集发现,该组数据的体重应该为58(kg).请重新根据最小二乘法的思想与公式,求出男体育特长生的身高与体重的线性回归方程.
参考公式: 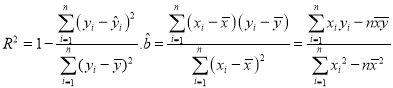 ,
,![]() .
.![]() .
.
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.