��Ŀ����
����Ŀ����ζƷƷ��ʦ����Ҫ�����ǶԸ���Ʒ�Ƶĵ�ζƷ����Ʒ�������������������䡢�з����ܶ���ʼ�������Ա�.�Ե�ζƷƷ��ʦ���˲��Ե�һ�ֳ��÷������£��ó�nƿ�����ͬ��Ʒ�ʲ�ͬ�ĵ�ζƷ����Ʒ����Ҫ���䰴Ʒ������Ϊ����������һ��ʱ�䣬������䵭��֮��������Ʒ����nƿ��ζƷ�������°�Ʒ������Ϊ�����������Ϊһ�ֲ���.����һ�ֲ����е����������ƫ��̶ȵĸߵ�Ϊ������.����![]() ���ֱ���
���ֱ���![]() ��
��![]() ��
��![]() ��
��![]() ��ʾ��һ������ʱ����Ϊ1��2��3��4�����ֵ�ζƷ�ڵڶ�������ʱ����ţ�����
��ʾ��һ������ʱ����Ϊ1��2��3��4�����ֵ�ζƷ�ڵڶ�������ʱ����ţ�����![]() ����X�Ƕ����������ƫ��̶ȵ�һ������.����ڶ�������ʱ�����Ϊ1��3��2��4����
����X�Ƕ����������ƫ��̶ȵ�һ������.����ڶ�������ʱ�����Ϊ1��3��2��4����![]() ��.
��.
��1��д��X�����п���ֵ���ɵļ��ϣ�
��2������![]() ��
��![]() ��
��![]() �����еȿ��ܵ�Ϊ1��2��3��4�ĸ������У���X����ѧ������
�����еȿ��ܵ�Ϊ1��2��3��4�ĸ������У���X����ѧ������
��3��ij��ζƷƷ��ʦ����̽��е����ֲ����У�����![]() .
.
��i������2���еĽ�������������������ĸ��ʣ��ٶ����ֲ������������
�����������жϸõ�ζƷƷ��ʦ��Ʒζ����������Σ���˵������.
���𰸡���1��![]() ��2��5��3��������
��2��5��3��������![]() ������������Ϊ��Ʒ��ʦȷ�������õ�ζ�������ܣ����ǿ�����²�.
������������Ϊ��Ʒ��ʦȷ�������õ�ζ�������ܣ����ǿ�����²�.
��������
��1����1��2��3��4��������ż�������������Ӷ�![]() ��
��![]() �������������
�������������![]() ��
��![]() �е�ż������������
�е�ż������������![]() ��
��![]() ����ż����ͬ���ɴ��ܾٳ�ʹ��X���п���ֵ���ɵļ���.
����ż����ͬ���ɴ��ܾٳ�ʹ��X���п���ֵ���ɵļ���.
��2�������б����г�1��2��3��4��һ��24�����У���÷ֲ��н������X����ѧ����.
��3������������![]() �������ֲ��Զ���
�������ֲ��Զ���![]() �ĸ��ʼ���p���ɶ����Լ�����������.
�ĸ��ʼ���p���ɶ����Լ�����������.
����������![]() ��һ����С�ĸ��ʣ�����������ƾ����²�õ����ֲ��Զ���
��һ����С�ĸ��ʣ�����������ƾ����²�õ����ֲ��Զ���![]() �Ľ���Ŀ����Ժ�С���Ӷ�������Ϊ��Ʒ��ʦȷ�������õ�ζ�������ܣ����ǿ�����²�.
�Ľ���Ŀ����Ժ�С���Ӷ�������Ϊ��Ʒ��ʦȷ�������õ�ζ�������ܣ����ǿ�����²�.
��1��X�Ŀ���ֵ����Ϊ![]() ��
��
��1��2��3��4��������ż������������
����![]() ��
��![]() �������������
�������������![]() ��
��![]() �е�ż��������
�е�ż��������
���![]() ��
��![]() ����ż����ͬ��
����ż����ͬ��
�Ӷ�![]() ��Ϊż����X��ֵ�Ǹ�������֪��ֵ������8.
��Ϊż����X��ֵ�Ǹ�������֪��ֵ������8.
�ɴ��ܾٳ�ʹ��X��ֵ����0��2��4��6��8��ֵ�����е�����.
��2�������б��г�1��2��3��4��һ��24�����У����±���ʾ��
|
|
|
|
|
|
|
|
|
| |
1 | 2 | 3 | 4 | 0 | 3 | 1 | 2 | 4 | 4 | |
1 | 2 | 4 | 3 | 2 | 3 | 1 | 4 | 2 | 6 | |
1 | 3 | 2 | 4 | 2 | 3 | 2 | 1 | 4 | 4 | |
1 | 3 | 4 | 2 | 4 | 3 | 2 | 4 | 1 | 6 | |
1 | 4 | 2 | 3 | 4 | 3 | 4 | 1 | 2 | 8 | |
1 | 4 | 3 | 2 | 4 | 3 | 4 | 2 | 1 | 8 | |
2 | 1 | 3 | 4 | 2 | 4 | 1 | 2 | 3 | 6 | |
2 | 1 | 4 | 3 | 4 | 4 | 1 | 3 | 2 | 6 | |
2 | 3 | 1 | 4 | 4 | 4 | 2 | 1 | 3 | 6 | |
2 | 3 | 4 | 1 | 6 | 4 | 2 | 3 | 1 | 6 | |
2 | 4 | 1 | 3 | 6 | 4 | 3 | 1 | 2 | 8 | |
2 | 4 | 3 | 1 | 6 | 4 | 3 | 2 | 1 | 8 |
����ÿ�������µ�Xֵ���ϱ���ʾ���ڵȿ��ܵļٶ��£��õ�
X | 0 | 2 | 4 | 6 | 8 |
P |
|
|
|
|
|
![]() .
.
��3������������![]() �������ֲ��Զ���
�������ֲ��Զ���![]() �ĸ��ʼ���p��
�ĸ��ʼ���p��
����������Ͷ����Լ��裬��![]() .
.
����������![]() ��һ����С�ĸ��ʣ�
��һ����С�ĸ��ʣ�
����������ƾ����²�õ����ֲ��Զ���![]() �Ľ���Ŀ����Ժ�С��
�Ľ���Ŀ����Ժ�С��
����������Ϊ��Ʒ��ʦȷ�������õ�ζ�������ܣ����ǿ�����²�.

 ��ս�п�����ϵ�д�
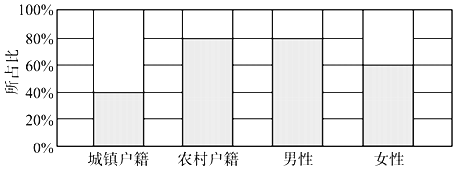
��ս�п�����ϵ�д�����Ŀ��ijУ������1������һ�����IJ��Խ�������ͬѧ���ڱ������ݷ���ʧ�ֽ�Ϊ����.Ϊ����������Ч���������γ��������硢����ʱ��վ���������ж���Ϊ�˽�ͬѧ�Ƕ�վ���������ж���̬�ȣ���ȫ��50��ͬѧ���е��飬�������������������Ƴ��±���
���Է��� |
|
|
|
|
|
|
Ƶ�� | 5 | 10 | 15 | 5 | 10 | 5 |
������ | 4 | 6 | 9 | 3 | 6 | 4 |
��1����ʹ����������Ϊ30%�������������Ӧ��Ϊ���ٷ֣�
��2�����ݵ�1�ʵĽ�������������о��Ƿ���վ���������ж���̬���뿼�Գɼ��Ƿ�����Ĺ�ϵ���г�2��2�����������ж��Ƿ���90%�İ�����Ϊ������̬����ɼ��Ƿ������й�ϵ.
�ο���ʽ�����ݣ�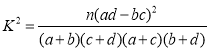 ��
��![]() .
.
| 0.100 | 0.050 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |